
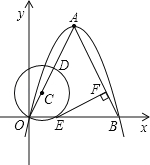
【题目】如图,已知A(2,4),以A为顶点的抛物线经过原点交x轴于B.
(1)求抛物线解析式;
(2)取OA上一点D,以OD为直径作⊙C交x轴于E,作EF⊥AB于F,求证EF是⊙C的切线;
(3)设⊙C半径为r,EF=m,求m与r的函数关系式及自变量r的取值范围;
(4)当⊙C与AB相切时,求⊙C半径r的值.
【答案】(1)y=﹣x2+4x.(2)详见解析;(3)![]() ;(4)
;(4)![]()
【解析】
(1)已知了抛物线顶点的坐标,可用顶点式的二次函数通式来设二次函数的解析式,将原点的坐标代入解析式中即可求出二次函数的解析式;
(2)要证EF是圆C的切线,那么可连接CE,证CE⊥EF即可,由于EF⊥AB,那么只需证明CE∥AB即可得出EF是切线的结论,那么OC=CE,根据抛物线的对称性可得OA=AB,由这两组相等的线段即可得出∠OEC=∠ABO,由此可得证;
(3)由(2)可知∠ABO=∠AOB,那么可通过三角函数来解,根据A,O,B的坐标不难得出∠AOB,∠ABO的正弦值,那么可过C作OB的垂线,垂足为M,可在直角三角形OCM中,用∠AOB的正切值以及r的长表示出OM,也就求出了OE,进而可表示出BE的长,然后在直角三角形BFE中,根据∠ABO的正弦值用BE表示出BF,由此可得出关于m,r的函数关系式;
(4)如果⊙C与AB相切,设切点为G,那么如果连接CG,四边形CEFG就是正方形,那么r=m=EF,那么根据(3)中m,r的函数关系式,将m=r代入(3)的函数关系式中即可求出r的值.
(1)设y=a(x﹣2)2+4,由于抛物线过原点(0,0),则有0=4a+4,
即a=﹣1.
因此抛物线的解析式为:y=﹣x2+4x;
(2)连CE,
则∠COE=∠CEO,
根据A是抛物线的顶点,可知OA=AB,即∠AOB=∠OBA,
∴∠OEC=∠ABO,
∴CE∥AB,又EF⊥AB,
∴CE⊥EF,
∴EF是⊙C的切线;
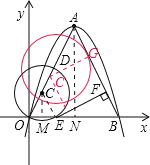
(3)分别过C、A作OB的垂线,垂足分别为M、N,
直角三角形OAN中,cos∠AOB=![]() ,
,
因此:OM=![]() ,OE=2OM=
,OE=2OM=![]() ,EB=4﹣
,EB=4﹣![]() ,
,
∴![]() (0<r<
(0<r<![]() );
);
(4)设⊙C切AB于点G,
连接CG,则CG⊥AB,
∴∠CGF=∠EFG=∠CEF=90°,
∴四边形CEFG为矩形,
又CE=CG,
∴四边形CEFG为正方形,
∴EF=r,
∴m=r①,
由(3)得![]() ,
,
解得r=![]() .
.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下折线统计图,则符合这一结果的实验最有可能的是( )

A. 袋中装有大小和质地都相同的3个红球和2个黄球,从中随机取一个,取到红球
B. 掷一枚质地均匀的正六面体骰子,向上的面的点数是偶数
C. 先后两次掷一枚质地均匀的硬币,两次都出现反面
D. 先后两次掷一枚质地均匀的正六面体骰子,两次向上的面的点数之和是7或超过9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图部分信息如下:
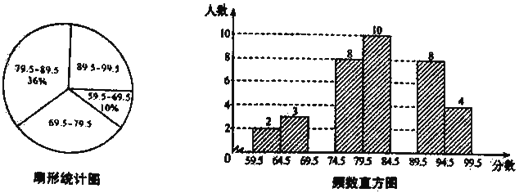
(1)本次比赛参赛选手共有 人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为 ;
(2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由;
(3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=5,BC=4,以A为圆心,3为半径作圆.试判断:
①点C与⊙A的位置关系;②点B与⊙A的位置关系;③AB中的D点与⊙A的位置关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD=∠ABC,补充一个条件,使得△ABD≌△ABC,则下列选项不符合题意的是( )
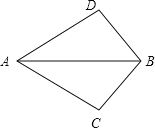
A. ∠D=∠CB. ∠DAB=∠CABC. BD=BCD. AD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
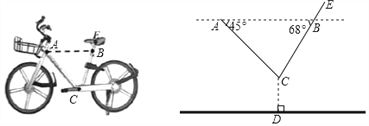
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)
查看答案和解析>>
科目:初中数学 来源: 题型:
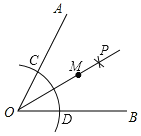
【题目】如图所示,∠AOB=70°,以点O为圆心,以适当长为半径作弧分别交OA,OB于C,D两点;分别以C,D为圆心,以大于![]() CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上取点M,连接MC、MD.若测得∠CMD=40°,则∠MDB=_____
CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上取点M,连接MC、MD.若测得∠CMD=40°,则∠MDB=_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量山坡上旗杆CD的高度,小明在点A处利用测角仪测得旗杆顶端D的仰角为37°,然后他沿着正对旗杆CD的方向前进17m到达B点处,此时测得旗杆顶部D和底端C的仰角分别为58°和30°,求旗杆CD的高度(结果精确到0.1m).
(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.6,sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC和△CDE都是等腰直角三角形,∠ACB=∠DCE=90°,且点A在ED的延长线上,以DE为直径的⊙O与AB交于G、H两点,连接BE.
(1)求证:BE是⊙O的切线;
(2)如图②,连接OB、OC,若tan∠CAD=![]() ,试判断四边形BECO的形状,请说明理由;
,试判断四边形BECO的形状,请说明理由;
(3)在(2)的条件下,若BF=![]() ,请你求出HG的长.
,请你求出HG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com