
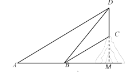
����Ŀ����ͼ��Ϊ�˲���ɽ�������CD�ĸ߶ȣ�С���ڵ�A�����ò���Dz����˶���D������Ϊ37����Ȼ���������������CD�ķ���ǰ��17m����B�㴦����ʱ�����˶���D�͵�C�����Ƿֱ�Ϊ58����30���������CD�ĸ߶ȣ������ȷ��0.1m����
���ο����ݣ�sin58���0.85��cos58���0.53��tan58���1.6��sin37���0.6��cos37���0.8��tan37���0.75��![]() ��1.73��
��1.73��

���𰸡����CD�ĸ߶�15.4m��
��������
�ӳ�CD��AB�ӳ��߽��ڵ�M����DM��x�����ɵõ�AM��![]() x��BM��
x��BM��![]() x��AM��BM��17���õ�DM=24,Ȼ��õ�BM��ֵ�����ɽ��
x��AM��BM��17���õ�DM=24,Ȼ��õ�BM��ֵ�����ɽ��
�⣺�ӳ�CD��AB�ӳ��߽��ڵ�M��
��DM��x��
��Rt��ADM����A��37����
��tan37����![]() ��
��
��AM��![]() x��
x��
��Rt��BDM����DBM��58����
��tan58����![]() ��
��
��BM��![]() x��
x��
��AM��BM��17��
x��24��
��BM��15��
��Rt��BCM����CBM��30����
tan30����![]() ��
��
��CM��5![]() ��
��
 ��DC��15.4m��
��DC��15.4m��
�����CD�ĸ߶�15.4m��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
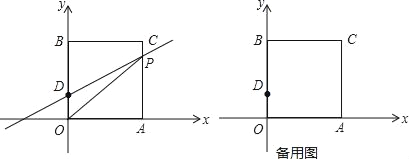
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�O������ԭ�㣬������OACB�Ķ���A��B�ֱ���x��y���ϣ���֪OA��3����DΪy����һ�㣬������Ϊ��0��1����CD��5����P�ӵ�A������ÿ��1����λ���ٶ����߶�A��C��B�ķ����˶�������P���B�غ�ʱֹͣ�˶����˶�ʱ��Ϊt��
��1����B��C�������ꣻ
��2��������OPD�����S����t�ĺ�����ϵʽ��
�ڵ���D����OP�ĶԳƵ�E����x����ʱ�����E�����ꣻ
��3���ڣ�2��������£�ֱ��OP����һ��F��ʹFE+FA��С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
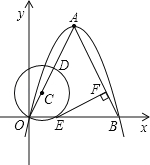
����Ŀ����ͼ����֪A��2��4������AΪ����������߾���ԭ�㽻x����B��
��1���������߽���ʽ��
��2��ȡOA��һ��D����ODΪֱ������C��x����E����EF��AB��F����֤EF�ǡ�C�����ߣ�
��3�����C�뾶Ϊr��EF��m����m��r�ĺ�����ϵʽ���Ա���r��ȡֵ��Χ��
��4������C��AB����ʱ�����C�뾶r��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣���ͼ����ABC�У���ACΪֱ������O���AB���ڵ�D����EΪ��O��һ�㣬����CE���ӳ���AB�ڵ�F������ED��
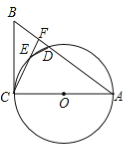
��1������B+��FED=90������֤��BC����O�����ߣ�
��2����FC=6��DE=3��FD=2������O��ֱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������ABCD��,AB=8,��B=60��,P��AB��һ��,BP=5,Q��CD���ϩ`����,���ı���APQD��ֱ��PQ�۵�,A�Ķ�Ӧ��A`.��CA`�ij�����Сʱ,��CQ�ij�Ϊ( )
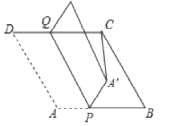
A. 7B. 2![]() C. 2
C. 2![]() D. 4
D. 4![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() �У�
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() Ϊ
Ϊ![]() ���ϵ��������㣬��
���ϵ��������㣬��![]() ������ʹ���ı���
������ʹ���ı���![]() ���ܳ���С����
���ܳ���С����![]() �ij���ӦΪ__________.
�ij���ӦΪ__________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ף����һ��ͯ�ڡ������꼶ͬѧ�ڰ��ν�����Ȥζ���С��ͬѧ��ģ���ϻ���һ������ABCD�������Ե�OΪ���İ�˳ʱ�뷽��ֱ���ת90�㣬180�㣬270���õ���ͼ��ʾ��ͼ�Σ����С�ABC��120�㣬AB��2cm��Ȼ��С�۽���ͼ��������һ�����ӣ���ô������Ͷ����ʱ������Ӱ���ֵĸ���Ϊ��������
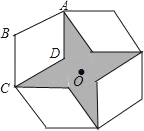
A. ![]() B. 2��
B. 2��![]() C.
C. ![]() -1D.
-1D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2+bx+c(a��0)�Ĵ���ͼ����ͼ��ʾ����������Ϊ(��2����9a)�����н��ۣ���abc��0����4a+2b+c��0����5a��b+c��0����������a(x+5)(x��1)����1��������x1��x2����x1��x2����5��x1��x2��1����������|ax2+bx+c|��2���ĸ����������ĸ����ĺ�Ϊ��4��������ȷ�Ľ�����( )
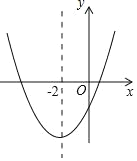
A. 2��B. 3��C. 4��D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֻ�������һ��A���ֻ�������һ��B���ֻ���õ������50Ԫ��������ͬ������A���ֻ���B���ֻ���õ�����ֱ�Ϊ3000Ԫ��2000Ԫ��
��1����ÿ��A���ֻ���B���ֻ�����������ֱ�Ϊ����Ԫ��
��2�����̵�ƻ�һ�ι��������ͺŵ��ֻ���110��������A���ֻ��Ľ�����������B���ֻ���2�����蹺��B���ֻ�n������110���ֻ�������������ΪyԪ��
����y����n�ĺ�����ϵʽ��
�ڸ��ֻ��깺��A�͡�B���ֻ������ٲ�������ʹ�������������
��3��ʵ�ʽ���ʱ�����Ҷ�B���ֻ��������µ�m��30��m��100��Ԫ�������̵�����B���ֻ�80̨�����̵걣�������ֻ����ۼ۲��䣬�������������Ϣ����2���е���������Ƴ�ʹ��110���ֻ��������������Ľ���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com