
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,△ABE与△ABO关于AB轴对称.
(1)求证:四边形AEBO是菱形;
(2)若AB=6,∠AOB=60°,求四边形AEBO的面积.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】小红和小明在操场做游戏,规则是:每人蒙上眼睛在一定距离外向设计好的图形内掷小石子,若掷中阴影部分则小红胜,否则小明胜,未掷入图形内则重掷一次.
(1)若第一次设计的图形(图1)是半径分别为20cm和30cm的同心圆.求游戏中小红获胜的概率你认为游戏对双方公平吗?请说明理由.
(2)若第二次设计的图形(图2)是两个矩形,其中大矩形的长为80cm、宽为60cm,且小矩形到矩形的边宽相等.要使游戏对双方公平,则边宽x应为多少cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公司有345台电脑需要一次性运送到某学校,计划租用甲、乙两种货车共8辆已知每辆甲种货车一次最多运送电脑45台、租车费用为400元,每辆乙种货车一次最多运送电脑30台、租车费用为280元
(Ⅰ)设租用甲种货车![]() 辆(
辆(![]() 为非负整数),试填写下表.
为非负整数),试填写下表.
表一:
租用甲种货车的数量/辆 | 3 | 7 |
|
租用的甲种货车最多运送电脑的数量/台 | 135 | ||
租用的乙种货车最多运送电脑的数量/台 | 150 |
表二:
租用甲种货车的数量/辆 | 3 | 7 |
|
租用甲种货车的费用/元 | 2800 | ||
租用乙种货车的费用/元 | 280 |
(Ⅱ)给出能完成此项运送任务的最节省费用的租车方案,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过点(﹣1,0),以下结论:①2a+b>0;②a+c<0;③4a+2b+c>0;④b2﹣5a2>2ac.其中正确的是( )
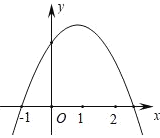
A. ①②B. ③④C. ②③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M(x0,y0)在x轴下方,对于以下说法:①b2﹣4ac>0②x=x0是方程ax2+bx+c=y0的解③x1<x0<x2④a(x0﹣x1)(x0﹣x2)<0其中正确的是( )
A.①③④B.①②④C.①②③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小方与小辉在玩军棋游戏,他们定义了一种新的规则,用军棋中的“工兵”、“连长”、“地雷”比较大小,共有6个棋子,分别为1个“工兵”,2个“连长”,3个“地雷”游戏规则如下:①游戏时,将棋反面朝上,两人随机各摸一个棋子进行比赛,先摸者摸出的棋不放回;②“工兵”胜“地雷”,“地雷”胜“连长”,“连长”胜“工兵”;③相同棋子不分胜负.
(1)若小方先摸,则小方摸到“排长”的事件是 ;若小方先摸到了“连长”,小辉在剩余的5个棋子中随机摸一个,则这一轮中小方胜小辉的概率为 .
(2)如果先拿走一个“连长”,在剩余的5个棋子中小方先摸一个棋子,然后小辉在剩余的4个棋子中随机摸一个,求这一轮中小方获胜的概率 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某教学活动小组选定测量小山上方某信号塔PQ的高度,他们在A处测得信号塔顶端P的仰角为45°,信号塔低端Q的仰角为31°,沿水平地面向前走100米到处,测得信号塔顶端P的仰角为68°.求信号塔PQ的高度.(结果精确到0.1米.参考数据:sin68°≈ 0.93,cos68° ≈ 0.37,tan68° ≈ 2.48,tan31° ≈ 0.60,sin31° ≈ 0.52,cos31°≈0.86)
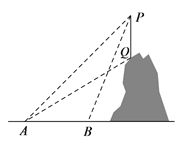
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=﹣x+1与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限,∠POQ=135°.
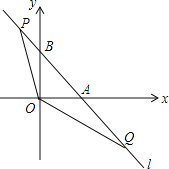
(1)求△AOB的周长;
(2)设AQ=t>0,试用含t的代数式表示点P的坐标;
(3)当动点P,Q在直线l上运动到使得△AOQ与△BPO的周长相等时,记tan∠AOQ=m,若过点A的二次函数y=ax2+bx+c同时满足以下两个条件:
①6a+3b+2c=0;
②当m≤x≤m+2时,函数y的最大值等于![]() ,求二次项系数a的值.
,求二次项系数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com