
����Ŀ����ͼ��ֱ��l��y=��x+1��x�ᣬy��ֱ���A��B���㣬��P��Q��ֱ��l�ϵ��������㣬�ҵ�P�ڵڶ����ޣ���Q�ڵ������ޣ���POQ=135�㣮
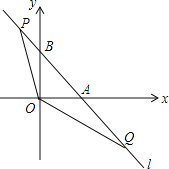
��1�����AOB���ܳ���
��2����AQ=t��0�����ú�t�Ĵ���ʽ��ʾ��P�����ꣻ
��3��������P��Q��ֱ��l���˶���ʹ�á�AOQ���BPO���ܳ����ʱ����tan��AOQ=m��������A�Ķ��κ���y=ax2+bx+cͬʱ������������������
��6a+3b+2c=0��
�ڵ�m��x��m+2ʱ������y�����ֵ����![]() ���������ϵ��a��ֵ��
���������ϵ��a��ֵ��
���𰸡���1����AOB�ܳ�Ϊ2+![]() ����2��P����
����2��P����![]() ��1+
��1+![]() ������3��a��ֵΪ
������3��a��ֵΪ![]() ��2
��2![]() ��2��
��2��
��������
�����������1�������A��B���꣬�����OB��OA��AB���ɽ�����⣮��2���ɡ�PBO�ס�OAQ����![]() =
=![]() �����PB���ٸ��ݵ���ֱ�����������ʿ�����õ�P���꣮��3�������m��ֵ���֢�a��0����a��0���������Σ����ö��κ������ʷֱ���⼴�ɣ�
�����PB���ٸ��ݵ���ֱ�����������ʿ�����õ�P���꣮��3�������m��ֵ���֢�a��0����a��0���������Σ����ö��κ������ʷֱ���⼴�ɣ�
�����������1���ں���y=��x+1�У���x=0����y=1��
��B��0��1����
��y=0����x=1��
��A��1��0����
��OA=OB=1��AB=![]() ��
��
���AOB�ܳ�Ϊ1+1+![]() =2+
=2+![]() ��
��
��2����OA=OB��
���ABO=��BAO=45�㣬
���PBO=��QAO=135�㣬
���POB=x�����OPB=��AOQ=135�㩁x��90��=45�㩁x��
���PBO�ס�OAQ��
��![]() =
=![]() ��
��
��PB=![]() =
=![]() ��
��
����P��PH��OB��H�㣬
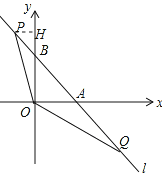
���PHBΪ����ֱ�������Σ�
��PB=![]() ��
��
��PH=HB=![]() ��
��
��P����![]() ��1+
��1+![]() ����
����
��3������2����֪��PBO�ס�OAQ�������ǵ��ܳ���ȣ������Ʊ�Ϊ1����ȫ�ȣ�
��PB=AQ��
��![]() =t��
=t��
��t��0��
��t=1��
ͬ���ɵ�Q��1+![]() ����
����![]() ����
����
��m=![]() =
=![]() ��1��
��1��
�������߾�����A��
��a+b+c=0��
�֡�6a+3b+2c=0��
��b=��4a��c=3a��
�Գ���x=2��ȡֵ��Χ![]() ��1��x
��1��x![]() +1��
+1��
����a��0�������ϣ�
������x=![]() ��1ʱȡ�����ֵ
��1ʱȡ�����ֵ![]() =2
=2![]() +2��
+2��
����![]() ��1��2a+��
��1��2a+��![]() ��1��b+c=2
��1��b+c=2![]() +2��
+2��
���a=![]() ��
��
����a��0�������£�
������x=2ʱȡ�����ֵ2![]() +2��
+2��
��4a+2b+c=2![]() +2��
+2��
���a=��2![]() ��2��
��2��
������������a��ֵΪ![]() ��2
��2![]() ��2��
��2��


 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
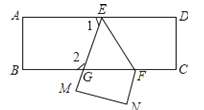
����Ŀ����һ�ų�����ֽƬABCD��EF�۵���ED��BC�Ľ���ΪG��D��C�ֱ���M��N��λ���ϣ�����EFG=55�㣬���1=______�㣬��2=_______�㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ഹֱ����������OE��OF�Ķ˵�O�����ǰ���ڲ��������ǰ�����ֱ�DZߵĽ���ֱ�Ϊ��D��B��
��1����գ�����ABO=50�㣬���ADO=������
��2����DC��BP�ֱ��ǡ�ADO����ABF�Ľ�ƽ���ߣ���ͼ1����֤��DC��BP��
��3����DC��BP�ֱ�ֱ��ǡ�ADE����ABF�Ľ�ƽ���ߣ���ͼ2������DC��BP��λ�ù�ϵ����˵�����ɣ�
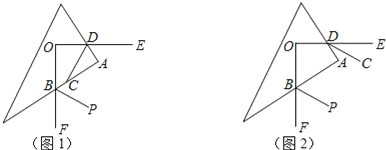
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����Ʒÿ���Ľ���Ϊ a Ԫ���ۼ�Ϊ���۵� 1.1 ������ÿ���ֽ���10Ԫ�����ۼ�Ϊÿ ��210Ԫ������������з���__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=8��BC=16��������ABCD��EF�۵���ʹ��C���A�غϣ����ۺ�EF�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˴ٽ�ѧ����������չ��ijУ��֯��չ�����Ż���ֱ������������ࡢ�����ࡢ��ѧ�༰���������ţ�Ҫ�����˲������ţ�ÿ��ֻ��ѡ��һ���Ϊ�˽�ѧ��ϲ���������Ż��ѧУ����һ�γ������飮�����ռ��������ݣ����Ƴ�����������������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺
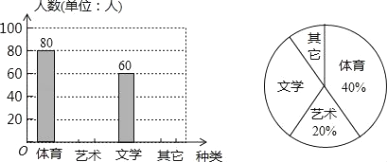
��1���˴ι������˶����ˣ�
��2������ѧ����������ͳ��ͼ����ռԲ�ĽǵĶ�����
��3���뽫����ͳ��ͼ����������
��4������У��1500��ѧ���������ϲ�����������ŵ�ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ����Rt��ABC��AC��Ϊֱ������O��б��AB�ڵ�E������EO���ӳ���BC���ӳ����ڵ�D����FΪBC���е㣬����EF��
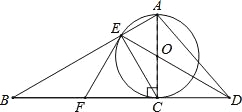
��1����֤��EF�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ3����EAC=60�㣬��AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��ԡ�һ��һ·�����߹��Ҳ��ϼӴ�Ͷ�ʣ�Ŀǰ��Ϊ�йع��Ҵ����˽�1100000000��Ԫ˰�գ�����1100000000�ÿ�ѧ��������ʾӦΪ��������
A. 0.11��108 B. 1.1��109 C. 1.1��1010 D. 11��108
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com