
【题目】如图,互相垂直的两条射线OE与OF的端点O在三角板的内部,与三角板两条直角边的交点分别为点D、B.
(1)填空:若∠ABO=50°,则∠ADO= ;
(2)若DC、BP分别是∠ADO、∠ABF的角平分线,如图1.求证:DC⊥BP;
(3)若DC、BP分别分别是∠ADE、∠ABF的角平分线,如图2.猜想DC与BP的位置关系,并说明理由.
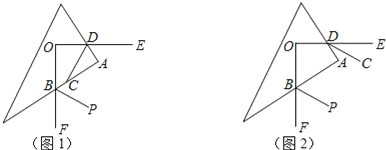
【答案】(1)130°;(2)证明见解析,(3)DC与BP互相平行.理由见解析.
【解析】试题分析:(1)由四边形的内角和为360°即可得;
(2)如图1,延长DC交BP于G,由∠OBA+∠ODA=180°、∠OBA+∠ABF=180°可得∠ODA=∠ABF,再由DC、BP分别是∠ADO、∠ABF的角平分线,从而可得∠CDA=∠CBG,再由∠DCA=∠BCG,继而可得∠BGC=∠A=90°,即得DC⊥BP;
(3)DC与BP互相平行.如图2,作过点A作AH∥BP,则可得∠ABP=∠BAH,由∠OBA+∠ODA=180°,可得∠ABF+∠ADE=180°,再由DC、BP分别分别是∠ADE、∠ABF的角平分线,从而可得∠ADC+∠ABP=90°,进而可得∠DAH=∠ADC,从而可得CD∥AH,最后得CD∥BP.
试题解析:(1)如图1,∵OE⊥OF,∴∠EOF=90°,
在四边形OBAD中,∠A=∠BOD=90°,∠ABO=50°,
∴∠ADO=360°﹣90°﹣90°﹣50°=130°;
故答案为:130°;
(2)如图1,延长DC交BP于G,
∵∠OBA+∠ODA=180°,而∠OBA+∠ABF=180°,∴∠ODA=∠ABF,
∵DC、BP分别是∠ADO、∠ABF的角平分线,∴∠CDA=∠CBG,
而∠DCA=∠BCG,∴∠BGC=∠A=90°,∴DC⊥BP;

(3)DC与BP互相平行.
理由:如图2,作过点A作AH∥BP,则∠ABP=∠BAH,
∵∠OBA+∠ODA=180°,∴∠ABF+∠ADE=180°,
∵DC、BP分别分别是∠ADE、∠ABF的角平分线,∴∠ADC+∠ABP=90°,
∴∠ADC+∠BAH=90°,
而∠DAH+∠BAH=90°,∴∠DAH=∠ADC,∴CD∥AH,∴CD∥BP.


科目:初中数学 来源: 题型:
【题目】冰冰家新安装了一台太阳能热水器,一天她测量发现18:00时,太阳能热水器水箱内水的温度是80℃,以后每小时下降4℃,第二天,冰冰早晨起来后测得水箱内水的温度为32℃,请你猜一猜她起床的时间是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列二次函数的图象与x轴有两个不同的交点的是( )
A. y=x2 B. y=x2+4 C. y=3x2﹣2x+5 D. y=3x2+5x﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
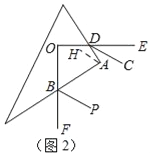
【题目】如图,在平面直角坐标系中,直线AB和抛物线交于点A(-4,0),B(0,4),且点B是抛物线的顶点.
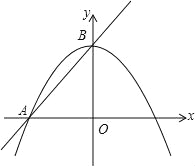
(1)求直线AB和抛物线的解析式.
(2)点P是直线上方抛物线上的一点,求当△PAB面积最大时点P的坐标.
(3)M是直线AB上一动点,在平面直角坐标系内是否存在点N,使以O、B、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
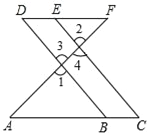
【题目】根据题意结合图形填空:如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.试说明:AC∥DF.将过程补充完整.
解:∵∠1=∠2(已知)
且∠1=∠3
∴∠2=∠3(等量代换)
∴ ∥
∴∠C=∠ABD
又∵∠C=∠D(已知)
∴ = (等量代换 )
∴AC∥DF .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=﹣x+1与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限,∠POQ=135°.
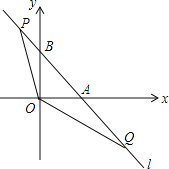
(1)求△AOB的周长;
(2)设AQ=t>0,试用含t的代数式表示点P的坐标;
(3)当动点P,Q在直线l上运动到使得△AOQ与△BPO的周长相等时,记tan∠AOQ=m,若过点A的二次函数y=ax2+bx+c同时满足以下两个条件:
①6a+3b+2c=0;
②当m≤x≤m+2时,函数y的最大值等于![]() ,求二次项系数a的值.
,求二次项系数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com