
【题目】小红和小明在操场做游戏,规则是:每人蒙上眼睛在一定距离外向设计好的图形内掷小石子,若掷中阴影部分则小红胜,否则小明胜,未掷入图形内则重掷一次.
(1)若第一次设计的图形(图1)是半径分别为20cm和30cm的同心圆.求游戏中小红获胜的概率你认为游戏对双方公平吗?请说明理由.
(2)若第二次设计的图形(图2)是两个矩形,其中大矩形的长为80cm、宽为60cm,且小矩形到矩形的边宽相等.要使游戏对双方公平,则边宽x应为多少cm?

科目:初中数学 来源: 题型:
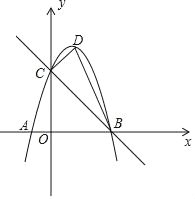
【题目】如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;
(3)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)与x轴交于A,B两点,顶点P(m,n).给出下列结论:①2a+c<0;②若(﹣![]() ,y1),(﹣
,y1),(﹣![]() ,y2),(
,y2),(![]() ,y3)在抛物线上,则y1>y2>y3;③关于x的方程ax2+bx+k=0有实数解,则k>c﹣n;④当n=﹣
,y3)在抛物线上,则y1>y2>y3;③关于x的方程ax2+bx+k=0有实数解,则k>c﹣n;④当n=﹣![]() 时,△ABP为等腰直角三角形.其中正确结论是______(填写序号).
时,△ABP为等腰直角三角形.其中正确结论是______(填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=![]() ∠A.
∠A.
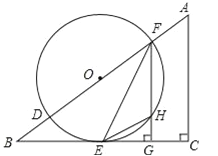
(1)求证:BC是⊙O的切线;
(2)若sinB=![]() ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx+1与抛物线y=x2-4x
(1)求证:直线l与该抛物线总有两个交点;
(2)设直线l与该抛物线两交点为A,B,O为原点,当k=-2时,求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
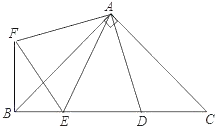
【题目】如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,∠EAD=45°,将△ADC绕点A顺时针旋转90°,得到△AFB,连接EF.
(1)求证:EF=ED;
(2)若AB=2![]() ,CD=1,求FE的长.
,CD=1,求FE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(某中学九年级学生共600人,其中男生320人,女生280人.该校对九年级所有学生进行了一次体育模拟测试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成如下的统计表:
类别 | 成绩(分) | 频数 | 频率 |
I | 40 | 36 | 0.3 |
II | 37—39 | a | b |
III | 34—36 | 24 | 0.2 |
IV | 31—33 | 6 | 0.05 |
合计 | c | 1 | |
(1)a= ; b= ;
(2)若将该表绘制成扇形统计图,那么Ⅲ类所对应的圆心角是 °;
(3)若随机抽取的学生中有64名男生和56名女生,请解释“随机抽取64名男生和56名女生”的合理性;
(4)估计该校九年级学生体育测试成绩是40分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,△ABE与△ABO关于AB轴对称.
(1)求证:四边形AEBO是菱形;
(2)若AB=6,∠AOB=60°,求四边形AEBO的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com