
【题目】如图,矩形OABC的顶点A、C的坐标分别是(4,0)和(0,2),反比例函数y= ![]() (x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为 .
(x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为 . 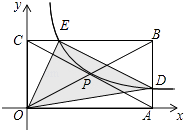
【答案】![]()
【解析】解:∵四边形OABC是矩形, ∴AB=OC,BC=OA,
∵A、C的坐标分别是(4,0)和(0,2),
∴OA=4,OC=2,
∵P是矩形对角线的交点,
∴P(2,1),
∵反比例函数y= ![]() (x>0)的图象过对角线的交点P,
(x>0)的图象过对角线的交点P,
∴k=2,
∴反比例函数的解析式为:y= ![]() ,
,
∵D,E两点在反比例函数y= ![]() (x>0)的图象的图象上,
(x>0)的图象的图象上,
∴D(4, ![]() ),E(1,2)
),E(1,2)
∴S阴影=S矩形﹣S△AOD﹣S△COF﹣S△BDE=4×2﹣ ![]() ×2﹣
×2﹣ ![]() ×2﹣
×2﹣ ![]() ×
× ![]() ×3=
×3= ![]() .
.
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用比例系数k的几何意义的相关知识可以得到问题的答案,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,将两个正方形(每个角都是![]() )的一个顶点重合放置,若
)的一个顶点重合放置,若![]() ,求
,求![]() 的度数;
的度数;
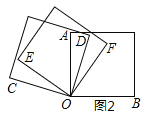
(2)如图2,将三个正方形的一个顶点重合放置,若![]() ,求
,求![]() 的度数;
的度数;
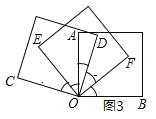
(3)如图3,将三个正方形的一个顶点重合放置,若![]() 平分
平分![]() ,那么
,那么![]() 平分
平分![]() 吗?为什么?
吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数y=ax2+bx+c(a≠0)的图象的顶点P的横坐标是4,图象交x轴于点A(m,0)和点B,且m>4,那么AB的长是( ) 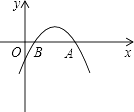
A.4+m
B.m
C.2m﹣8
D.8﹣2m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论: ①2a+b=0;
②abc>0;
③方程ax2+bx+c=3有两个相等的实数根;
④抛物线与x轴的另一个交点是(﹣1,0);
⑤当1<x<4时,有y2<y1 ,
其中正确的是( )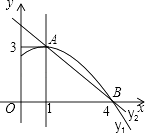
A.①②③
B.①③④
C.①③⑤
D.②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将腰CD以D为中心逆时针旋转90°至DE,连接AE、CE,△ADE的面积为3,则BC的长为____________.
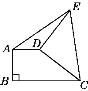
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批单价为4元的日用品.若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数y(件)与价格x(元/件)之间满足一次函数关系.
(1)试求y与x之间的函数关系式;
(2)当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A,B,把抛物线与线段AB围成的图形记为C1 , 将Cl绕点B中心对称变换得C2 , C2与x轴交于另一点C,将C2绕点C中心对称变换得C3 , 连接C,与C3的顶点,则图中阴影部分的面积为( ) 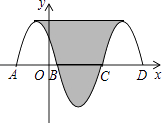
A.32
B.24
C.36
D.48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4 ![]() 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( ) 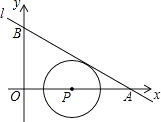
A.6
B.8
C.10
D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com