
【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4 ![]() 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( ) 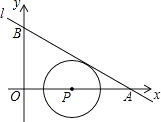
A.6
B.8
C.10
D.12
【答案】A
【解析】解:∵直线l:y=kx+4 ![]() 与x轴、y轴分别交于A、B, ∴B(0,4
与x轴、y轴分别交于A、B, ∴B(0,4 ![]() ),
),
∴OB=4 ![]() ,
,
在RT△AOB中,∠OAB=30°,
∴OA= ![]() OB=
OB= ![]() ×
× ![]() =12,
=12,
∵⊙P与l相切,设切点为M,连接PM,则PM⊥AB,
∴PM= ![]() PA,
PA,
设P(x,0),
∴PA=12﹣x,
∴⊙P的半径PM= ![]() PA=6﹣
PA=6﹣ ![]() x,
x,
∵x为整数,PM为整数,
∴x可以取0,2,4,6,8,10,6个数,
∴使得⊙P成为整圆的点P个数是6.
故选:A.
根据直线的解析式求得OB=4 ![]() ,进而求得OA=12,根据切线的性质求得PM⊥AB,根据∠OAB=30°,求得PM=
,进而求得OA=12,根据切线的性质求得PM⊥AB,根据∠OAB=30°,求得PM= ![]() PA,然后根据“整圆”的定义,即可求得使得⊙P成为整圆的点P的坐标,从而求得点P个数.
PA,然后根据“整圆”的定义,即可求得使得⊙P成为整圆的点P的坐标,从而求得点P个数.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C的坐标分别是(4,0)和(0,2),反比例函数y= ![]() (x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为 .
(x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为 . 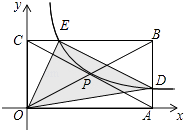
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年9月5日,二十国集团领导人杭州峰会在杭州国际博览中心继续举行,这次峰会吸引了大批游客在“十一”假期间前往杭州旅游.为抓住商机,两个商家对同样一件售价为50元/个的产品进行促销活动.甲商家用如下方法促销:若购买该商品不超过l0个,按原价付款:若一次购买l0个以上.且购买的个数每增加一个,其价格减少l元,但该商品的售价不得低于35元/个;乙店一律按原价的80%销售.现购买该商品x个,如果全部在甲商家购买,则所需金额为y1元:如果全部在乙商家购买,则所需金额为y2元.
(1)分别求出yl , y2与x之间的函数关系式;
(2)若一位游客花800元,最多能购买多少个该商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
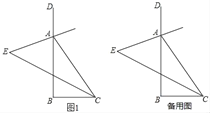
【题目】如图1,在△ABC中,∠B=90°,分别作其内角∠ACB与外角∠DAC的平分线,且两条角平分线所在的直线交于点E.
(1)∠E= °;
(2)分别作∠EAB与∠ECB的平分线,且两条角平分线交于点F.
①依题意在图1中补全图形;
②求∠AFC的度数;
(3)在(2)的条件下,射线FM在∠AFC的内部且∠AFM=![]() ∠AFC,设EC与AB的交点为H,射线HN在∠AHC的内部且∠AHN=
∠AFC,设EC与AB的交点为H,射线HN在∠AHC的内部且∠AHN=![]() ∠AHC,射线HN与FM交于点P,若∠FAH,∠FPH和∠FCH满足的数量关系为∠FCH=m∠FAH+n∠FPH,请直接写出m,n的值.
∠AHC,射线HN与FM交于点P,若∠FAH,∠FPH和∠FCH满足的数量关系为∠FCH=m∠FAH+n∠FPH,请直接写出m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠(在几何里叫做平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
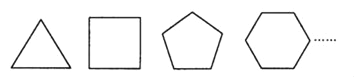
(1)请根据下列图形,填写表中空格:
正多边形边数 | 3 | 4 | 5 | 6 | … |
正多边形每个内角的度数 | … |
(2)如图,如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形;
(3)正三角形、正四边形、正六边形中选一种,再在其他正多边形中选一种,请画出用这两种不同的正多边形镶嵌成的一个平面图形(草图);并探索这两种正多边形共能镶嵌成几种不同的平面图形?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A的坐标为(﹣2,0),OB=OA,且∠AOB=120°.
(1)求经过A,O,B三点的抛物线的解析式.
(2)在(1)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(3)若点M为抛物线上一点,点N为对称轴上一点,是否存在点M,N使得A,O,M,N构成的四边形是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2 , b1≠b2 , 那么称这两个一次函数为“平行一次函数”. 如图,已知函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=﹣2x+4是“平行一次函数”
(1)若函数y=kx+b的图象过点(3,1),求b的值;
(2)若函数y=kx+b的图象与两坐标轴围成的三角形和△AOB构成位似图形,位似中心为原点,位似比为1:2,求函数y=kx+b的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com