
【题目】在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠(在几何里叫做平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
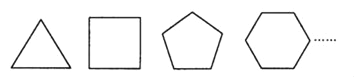
(1)请根据下列图形,填写表中空格:
正多边形边数 | 3 | 4 | 5 | 6 | … |
正多边形每个内角的度数 | … |
(2)如图,如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形;
(3)正三角形、正四边形、正六边形中选一种,再在其他正多边形中选一种,请画出用这两种不同的正多边形镶嵌成的一个平面图形(草图);并探索这两种正多边形共能镶嵌成几种不同的平面图形?说明你的理由.
【答案】(1)见解析;(2)正三角形、正四边形(或正方形)、正六边形;(3)符合条件的图形只有一种.
【解析】
本题主要考查了平面镶嵌(密铺).(1)利用正多边形一个内角="180-"![]() 求解;
求解;
(2)进行平面镶嵌就是在同一顶点处的几个多边形的内角和应为360°,因此我们只需验证360°是不是上面所给的几个正多边形的一个内角度数的整数倍;
(3)常见的两种正多边形的密铺组合有:正三角形和正四边形能密铺,正六边形只能和正三角形密铺.所以要从正三角形、正四边形、正六边形中选一种,只能选择正四边形.
解:(1)由正n边形的内角的性质可分别求得正三角形、正方形、正五边形、正六边形、…、正n边形的每一个内角为:
60°,90°,108°,120°,…![]() ;
;
(2)如限于用一种正多边形镶嵌,则由一顶点的周围角的和等于360°得正三角形、正四边形(或正方形)、正六边形都能镶嵌成一个平面图形;
(3)如:正方形和正八边形(如图),
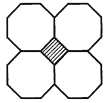
设在一个顶点周围有m个正方形的角,n个正八边形的角,
那么m,n应是方程m90°+n135°=360°的正整数解.
即2m+3n=8的正整数解,只有m=1,n=2一组,
∴符合条件的图形只有一种.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将腰CD以D为中心逆时针旋转90°至DE,连接AE、CE,△ADE的面积为3,则BC的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中任意一点p(x,y)经平移后对应点为p1(x+5,y+3),将△ABC作同样的平移得到△A1B1C1.
(1)画出△A1B1C1;
(2)求A1,B1,C1的坐标;
(3)写出平移的过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.

(1)∠1与∠2有什么关系,为什么?
(2)BE与DF有什么关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4 ![]() 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( ) 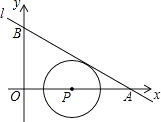
A.6
B.8
C.10
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,这是一个五角星ABCDE,你能计算出∠A+∠B+∠C+∠D+∠E的度数吗?为什么?(必须写推理过程)
(2)如图2,如果点B向右移动到AC上,那么还能求出∠A+∠DBE+∠C+∠D+∠E的大小吗?若能结果是多少?(可不写推理过程)
(3)如图,当点B向右移动到AC的另一侧时,上面的结论还成立吗?
(4)如图4,当点B、E移动到∠CAD的内部时,结论又如何?根据图3或图4,说明你计算的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次男子马拉松长跑比赛中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据:140 146 143 175 125 164 134 155 152 168 162 148
(1)计算该样本数据的中位数和平均数;
(2)如果一名选手的成绩是147分钟,请你依据样本数据的中位数,推断他的成绩如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月,举世瞩目的“一带一路”国际合作高峰论坛在北京举行.为了让学生更深刻地了解这一普惠世界的中国创举,某校组织八年级甲班和乙班的学生开展“一带一路”知识竞赛活动.现场决赛时,甲班和乙班分别选5名同学参加比赛,成绩如图所示:

(1)根据上图将计算结果填入下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | _____ | _____ |
乙班 | 8.5 | ______ | 10 | 1.6 |
(2)你认为哪个班的成绩较好?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意,解答问题:
(1)如图1,已知直线y=2x+4与x轴、y轴分别交于A、B两点,求线段AB的长.
(2)如图2,类比(1)的解题过程,请你通过构造直角三角形的方法,求出点M(3,4)与点N(﹣2,﹣1)之间的距离.
(3)在(2)的基础上,若有一点D在x轴上运动,当满足DM=DN时,请求出此时点D的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com