
【题目】根据题意,解答问题:
(1)如图1,已知直线y=2x+4与x轴、y轴分别交于A、B两点,求线段AB的长.
(2)如图2,类比(1)的解题过程,请你通过构造直角三角形的方法,求出点M(3,4)与点N(﹣2,﹣1)之间的距离.
(3)在(2)的基础上,若有一点D在x轴上运动,当满足DM=DN时,请求出此时点D的坐标.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)点D的坐标为(2,0).
;(3)点D的坐标为(2,0).
【解析】分析:(1)由一次函数解析式求得点A、B的坐标,则易求直角△AOB的两直角边OB、OA的长度,所以在该直角三角形中利用勾股定理即可求线段AB的长度;
(2)如图2,过M点作x轴的垂线MF,过N作y轴的垂线NE,MF和NE交于点C,构造直角△MNC,则在该直角三角形中利用勾股定理来求求点M与点N间的距离;
(3)如图3,设点D坐标为(m,0),连结ND,MD,过N作NG垂直x轴于G,过M作MH垂直x轴于H.在直角△DGN和直角△MDH中,利用勾股定理得到关于m的方程12+(m+2)=42+(3-m)2
通过解方程即可求得m的值,则易求点D的坐标.
详解:(1)令x=0,得y=4,即A(0,4).
令y=0,得x=-2,即B(-2,0).
在Rt△AOB中,根据勾股定理有:
AB=![]() ;
;
(2)如图2,过M点作x轴的垂线MF,过N作y轴的垂线NE,MF和NE交于点C.
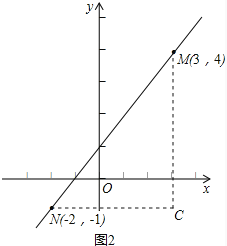
根据题意:MC=4-(-1)=5,NC=3-(-2)=5.
则在Rt△MCN中,根据勾股定理有:
MN=![]() ;
;
(3)如图3,设点D坐标为(m,0),连结ND,MD,

过N作NG垂直x轴于G,过M作MH垂直x轴于H.
则GD=|m-(-2)|,GN=1,DN2=GN2+GD2=12+(m+2)2
MH=4,DH=|3-m|,DM2=MH2+DH2=42+(3-m)2
∵DM=DN,
∴DM2=DN2
即12+(m+2)=42+(3-m)2
整理得:10m=20得m=2
∴点D的坐标为(2,0).


科目:初中数学 来源: 题型:
【题目】如图所示,将一张正方形纸片剪成四个大小一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去。
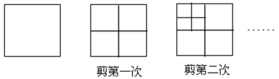
(1)完成下表:
剪的次数 | 1 | 2 | 3 | 4 | 5 | ... | n |
小正方形的个数 | 4 | 7 | 10 | ... |
|
(2)![]() .(用含n的代数式表示)
.(用含n的代数式表示)
(3)按上述方法,能否得到2018个小正方形?如果能,请求出n;如不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A为半圆O直径MN所在直线上一点,射线AB垂直于MN,垂足为A,半圆绕M点顺时针转动,转过的角度记作a;设半圆O的半径为R,AM的长度为m,回答下列问题: 
(1)探究:若R=2,m=1,如图1,当旋转30°时,圆心O′到射线AB的距离是;如图2,当a=°时,半圆O与射线AB相切;
(2)如图3,在(1)的条件下,为了使得半圆O转动30°即能与射线AB相切,在保持线段AM长度不变的条件下,调整半径R的大小,请你求出满足要求的R,并说明理由.
(3)发现:如图4,在0°<α<90°时,为了对任意旋转角都保证半圆O与射线AB能够相切,小明探究了cosα与R、m两个量的关系,请你帮助他直接写出这个关系;cosα=(用含有R、m的代数式表示)
(4)拓展:如图5,若R=m,当半圆弧线与射线AB有两个交点时,α的取值范围是 , 并求出在这个变化过程中阴影部分(弓形)面积的最大值(用m表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:

(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,点E在BC边上,且CE=2,AE与BD交于点F,连接CF,则下列结论不正确的是( ) 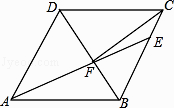
A.△ABF≌△CBF
B.△ADF∽△EBF
C.tan∠EAB= ![]()
D.S△EAB=6 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃容器高19cm,底面周长为60cm,在外侧距下底1.5cm的点A处有一只蜘蛛,在蜘蛛正对面的圆柱形容器的外侧,距上底1.5cm处的点B处有一只苍蝇,蜘蛛急于捕捉苍蝇充饥,请你帮蜘蛛计算它沿容器侧面爬行的最短距离.
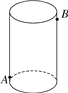
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,经过点A作AE⊥OC,垂足为点D,AE与BC交于点F,与过点B的直线交于点E,且EB=EF. 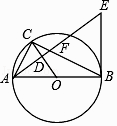
(1)求证:BE是⊙O的切线;
(2)若CD=1,cos∠AEB= ![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3,P是AC上一动点,则PB+PE的最小值是( ).
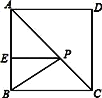
A. 5 B. 5![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,射线BC∥射线OA,∠C=∠BAO=100°,试回答下列问题:
(1)如图①,求证:OC∥AB;
(2)若点E、F在线段BC上,且满足∠EOB=∠AOB,并且OF平分∠BOC,
①如图②,若∠AOB=30°,则∠EOF的度数等于多少(直接写出答案即可);
②若平行移动AB,当∠BOC=6∠EOF时,求∠ABO.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com