
����Ŀ����ͼ1������ABC�У���B=90�����ֱ������ڽǡ�ACB����ǡ�DAC��ƽ���ߣ���������ƽ�������ڵ�ֱ�߽��ڵ�E��
��1����E=�� ���㣻
��2���ֱ�����EAB���ECB��ƽ���ߣ���������ƽ���߽��ڵ�F��
����������ͼ1�в�ȫͼ�Σ�
�����AFC�Ķ�����
��3���ڣ�2���������£�����FM�ڡ�AFC���ڲ��ҡ�AFM=![]() ��AFC����EC��AB�Ľ���ΪH������HN�ڡ�AHC���ڲ��ҡ�AHN=
��AFC����EC��AB�Ľ���ΪH������HN�ڡ�AHC���ڲ��ҡ�AHN=![]() ��AHC������HN��FM���ڵ�P������FAH����FPH�͡�FCH�����������ϵΪ��FCH=m��FAH+n��FPH����ֱ��д��m��n��ֵ��
��AHC������HN��FM���ڵ�P������FAH����FPH�͡�FCH�����������ϵΪ��FCH=m��FAH+n��FPH����ֱ��д��m��n��ֵ��
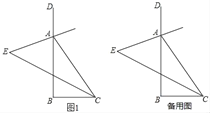
���𰸡���1��45����2��67.5�㣻��3��m=2��n=��3��
��������
��1�����ݽ�ƽ���ߵĶ���ɵá�CAF=![]() ��DAC����ACE=
��DAC����ACE=![]() ��ACB�����CAF=x����ACE=y��������֪���Ƶ��ó�x��y=45���ٸ�����������ǵ����ʼ�����ô𰸣�
��ACB�����CAF=x����ACE=y��������֪���Ƶ��ó�x��y=45���ٸ�����������ǵ����ʼ�����ô𰸣�
��2���ٸ��ݽ�ƽ���ߵij߹���ͼ�ķ�������ͼ�μ��ɣ�
����ͼ2����CFƽ�֡�ECB�ɵá�ECF=![]() y���ٸ��ݡ�E+��EAF=��F+��ECF�Լ���E+��EAB=��B+��ECB�����Ƶ��ó�45��+
y���ٸ��ݡ�E+��EAF=��F+��ECF�Լ���E+��EAB=��B+��ECB�����Ƶ��ó�45��+![]() =��F+
=��F+![]() y���ɴ˼�����ô𰸣�
y���ɴ˼�����ô𰸣�
��3����ͼ3�����FAH=��������AFƽ�֡�EAB�ɵá�FAH=��EAF=����������֪���Ƶ��ó���FCH=����22.5������+22.5=30+![]() ��FCH+��FPH�ڣ��ɴ˿ɵá�FPH=
��FCH+��FPH�ڣ��ɴ˿ɵá�FPH=![]() ���ٸ��ݡ�FCH=m��FAH+n��FPH��������ô�.
���ٸ��ݡ�FCH=m��FAH+n��FPH��������ô�.
��1����ͼ1��
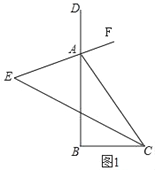
��EAƽ�֡�DAC��ECƽ�֡�ACB��
���CAF=![]() ��DAC����ACE=
��DAC����ACE=![]() ��ACB��
��ACB��
���CAF=x����ACE=y��
�ߡ�B=90�㣬
���ACB+��BAC=90�㣬
��2y+180��2x=90��
x��y=45��
�ߡ�CAF=��E+��ACE��
���E=��CAF����ACE=x��y=45�㣬
�ʴ�Ϊ��45��
��2������ͼ2��ʾ��
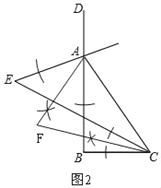
����ͼ2����CFƽ�֡�ECB��
���ECF=![]() y��
y��
�ߡ�E+��EAF=��F+��ECF��
��45��+��EAF=��F+![]() y ����
y ����
ͬ���ɵã���E+��EAB=��B+��ECB��
��45��+2��EAF=90��+y��
���EAF=![]() ����
����
�Ѣڴ���ٵã�45��+![]() =��F+
=��F+![]() y��
y��
���F=67.5�㣬
����AFC=67.5�㣻
��3����ͼ3�����FAH=����
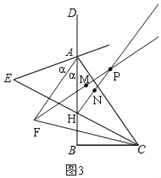
��AFƽ�֡�EAB��
���FAH=��EAF=����
�ߡ�AFM=![]() ��AFC=
��AFC=![]() ��67.5��=22.5�㣬
��67.5��=22.5�㣬
�ߡ�E+��EAF=��AFC+��FCH��
��45+��=67.5+��FCH��
���FCH=����22.5����
�ߡ�AHN=![]() ��AHC=
��AHC=![]() ����B+��BCH��=
����B+��BCH��=![]() ��90+2��FCH��=30+
��90+2��FCH��=30+![]() ��FCH��
��FCH��
�ߡ�FAH+��AFM=��AHN+��FPH��
����+22.5=30+![]() ��FCH+��FPH����
��FCH+��FPH����
�Ѣٴ���ڵã���FPH=![]() ��
��
�ߡ�FCH=m��FAH+n��FPH��
����22.5=m��+n![]() ��
��
��ã�m=2��n=��3��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y1=ax2+bx+c��a��0��ͼ���һ���֣������ߵĶ�������A��1��3������x���һ������B��4��0����ֱ��y2=mx+n��m��0���������߽���A��B���㣬���н��ۣ� ��2a+b=0��
��abc��0��
�۷���ax2+bx+c=3��������ȵ�ʵ������
����������x�����һ�������ǣ���1��0����
�ݵ�1��x��4ʱ����y2��y1 ��
������ȷ���ǣ� ��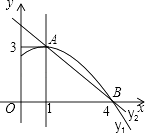
A.�٢ڢ�
B.�٢ۢ�
C.�٢ۢ�
D.�ڢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��3���������������Ϸ���ö���ӣ���ͼ��ʾ��λ�ü���������ö���ӣ�������ö�������������������ϣ���������ö�������ڵĸ��Ϊ�������������ֱ�������εĸ���Ϊ �� 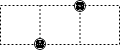
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+2x+3��y�ύ�ڵ�C����D��0��1������P���������ϵĶ��㣮����PCD����CDΪ�ĵ��������Σ����P������Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Rt��ABC�У���C=90�㣬��D��E�ֱ��ǡ�ABC��AC��BC�ϵĵ㣬��P��һ���㣮���PDA=��1����PEB=��2����DPE=�Ϧ���

��1������P���߶�AB�ϣ���ͼ��1����ʾ���ҡϦ�=50�㣬���1+��2= �㣻
��2������P�ڱ�AB���˶�����ͼ��2����ʾ����Ϧ�����1����2֮���кι�ϵ��˵��������
��3������P��Rt��ABCб��BA���ӳ������˶���CE��CD������Ϧ�����1����2֮���кι�ϵ�����벢˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǽ���ֱ������ϵ��Բ������Ͱ뾶��Ϊ������Բ��Ϊ����Բ������ͼ��ֱ��l��y=kx+4 ![]() ��x�ᡢy��ֱ���A��B����OAB=30�㣬��P��x���ϣ���P��l���У���P���߶�OA���˶�ʱ��ʹ�á�P��Ϊ��Բ�ĵ�P�����ǣ� ��
��x�ᡢy��ֱ���A��B����OAB=30�㣬��P��x���ϣ���P��l���У���P���߶�OA���˶�ʱ��ʹ�á�P��Ϊ��Բ�ĵ�P�����ǣ� �� 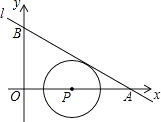
A.6
B.8
C.10
D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶��ѧ��ȤС�龭���г����飬�õ�ij���˶���ÿ�µ��������ۼ۵������Ϣ���±���
�ۼۣ�Ԫ/���� | 100 | 110 | 120 | 130 | �� |
������������ | 200 | 180 | 160 | 140 | �� |
��֪���˶����Ľ���Ϊÿ��60Ԫ�����ۼ�ΪxԪ��
��1�����ú�x��ʽ�ӱ�ʾ�������۸��˶���ÿ���������� ����Ԫ������������ ����������ֱ��д�������
��2�������۸��˶�����������ΪyԪ����ô�ۼ�Ϊ����ʱ�����µ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������̿���һ�����ţ�����۵꣬��Ҫ��Ӫ�����ѧ���������������ţ�����������ԭζ���������ھ�Ӫ���ƣ���������ţ��������û���꣩������������������Ϊ��ϸ�ĵ�С������ѧ֪ʶ������ͳ����һ������ţ�̵���������������Ƴ��±���
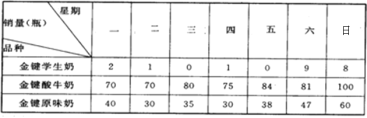
��1�������Ʒ��ţ�̵���ƽ������������˵������ţ�����������
��2�������Ʒ��ţ�̵ķ��������λС���������Ƚ�����ţ���������ȶ���
��3����������С�죬���������Щ����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=6��BC=8����E��BC����һ�㣬����AE���ѡ�B��AE�۵���ʹ��B���ڵ�B�䴦������CEB��Ϊֱ��������ʱ��BE�ij�Ϊ �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com