
【题目】如图,在直角坐标系中,点A的坐标为(﹣2,0),OB=OA,且∠AOB=120°.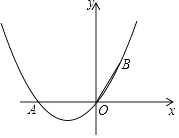
(1)求经过A,O,B三点的抛物线的解析式.
(2)在(1)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(3)若点M为抛物线上一点,点N为对称轴上一点,是否存在点M,N使得A,O,M,N构成的四边形是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】
(1)
解:过点B作BD⊥x轴于点D,由已知可得:OB=OA=2,∠BOD=60°,
在Rt△OBD中,∠ODB=90°,∠OBD=30°
∴OD=1,DB= ![]()
∴点B的坐标是(1, ![]() ).
).
设所求抛物线的解析式为y=ax2+bx+c,
由已知可得: 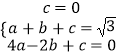 ,
,
解得: 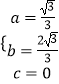
∴所求抛物线解析式为y= ![]() .
.
(2)
解:存在,
∵△BOC的周长=OB+BC+CO,
又∵OB=2
∴要使△BOC的周长最小,必须BC+CO最小,
∵点O和点A关于对称轴对称
∴连接AB与对称轴的交点即为点C,
且有OC=OA
此时△BOC的周长=OB+BC+CO=OB+BC+AC;
点C为直线AB与抛物线对称轴的交点
设直线AB的解析式为y=kx+b,
将点A(﹣2,0),B(1, ![]() )分别代入,得:
)分别代入,得:
![]() ,
,
解得: 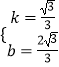 ,
,
∴直线AB的解析式为y= ![]() x+
x+ ![]()
当x=﹣1时,y= ![]() ,
,
∴所求点C的坐标为(﹣1, ![]() );
);
(3)
解:如图,
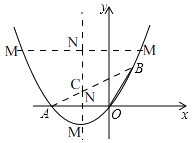
①当以OA为对角线时,
OA与MN互相垂直且平分
∴点M(﹣1,﹣ ![]() ),
),
②当以OA为边时
OA=MN且OA∥MN
即MN=2,MN∥x轴
设N(﹣1,t)
则M(﹣3,t)或(1,t)
将M点坐标代入y= ![]() .
.
∴t= ![]()
∴M(﹣3, ![]() )或(1,
)或(1, ![]() )
)
综上:点M的坐标为:M(﹣1,﹣ ![]() )或(﹣3,
)或(﹣3, ![]() )或(1,
)或(1, ![]() ).
).
【解析】(1)先确定出点B坐标,再用待定系数法即可;(2)先判断出使△BOC的周长最小的点C的位置,再求解即可;(3)分OA为对角线和为边两种情况进行讨论计算.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场购进一批单价为4元的日用品.若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数y(件)与价格x(元/件)之间满足一次函数关系.
(1)试求y与x之间的函数关系式;
(2)当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4 ![]() 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( ) 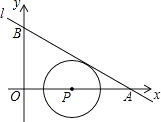
A.6
B.8
C.10
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 ()元;②月销量是 ()件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次男子马拉松长跑比赛中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据:140 146 143 175 125 164 134 155 152 168 162 148
(1)计算该样本数据的中位数和平均数;
(2)如果一名选手的成绩是147分钟,请你依据样本数据的中位数,推断他的成绩如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红的奶奶开了一个金键牛奶销售店,主要经营“金键学生奶”、“金键酸牛奶”、“金键原味奶”,由于经营不善,经常导致牛奶滞销(没卖完)或脱销(量不够),为此细心的小红结合所学知识帮奶奶统计了一个星期牛奶的销售情况,并绘制成下表:
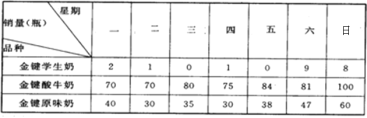
(1)计算各品种牛奶的日平均销售量,并说明哪种牛奶销量最高;
(2)计算各品种牛奶的方差(保留两位小数),并比较哪种牛奶销量最稳定;
(3)假如你是小红,会给奶奶哪些建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中∠ABC=90°,∠A=30°,BC=2cm,动点P以3cm/s的速度由A沿射线AC方向运动,动点Q同时以1cm/s的速度由B向CB的延长线方向运动,连PQ交直线AB于D,则当运动时间为s时,△ADP是等腰三角形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题。 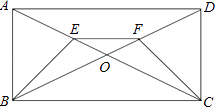
(1)用适当的方法解下列一元二次方程:x2﹣6x+1=0.
(2)如图,已知E、F分别是矩形ABCD的对角线AC和BD上的点,且AE=DF,求证:BE=CF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com