
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若$\sqrt{x^2}=5$,则x=5 | |
| B. | 若a(a≥0)为有理数,则$\sqrt{a}$是它的算术平方根 | |
| C. | 化简$\sqrt{{{(3-π)}^2}}$的结果是π-3 | |
| D. | 若二次根式$\frac{2}{\sqrt{x+1}}$有意义,则x的取值范围为x>-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3$\sqrt{3}$).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动,速度分别为1,$\sqrt{3}$,2(长度单位/秒).一直尺的上边缘l从x轴的位置开始以$\frac{\sqrt{3}}{3}$(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3$\sqrt{3}$).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动,速度分别为1,$\sqrt{3}$,2(长度单位/秒).一直尺的上边缘l从x轴的位置开始以$\frac{\sqrt{3}}{3}$(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
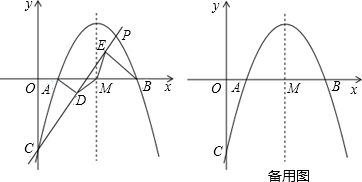
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com