练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，等腰三角形底边的长为，面积是，腰的垂直平分线交于点，若为边上的中点，为线段上一动点，则的周长的最小值为（ ）

    A.B.C.D.

    【答案】D

    【解析】

    连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再根据EF是线段AB的垂直平分线可知，点B关于直线EF的对称点为点A，故AD的长为BM+MD的最小值，由此即可得出结论．

    连接AD，

    ∵△ABC是等腰三角形，点D是BC边的中点，

    ∴AD⊥BC，

    ∴S△ABC=BCAD=×4×AD=12，解得AD=6cm，

    ∵EF是线段AB的垂直平分线，

    ∴点B关于直线EF的对称点为点A，

    ∴AD的长为BM+MD的最小值，

    ∴△BDM的周长最短=（BM+MD）+BD=AD+BC=6+×4=6+=8cm．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB=AC，EB=EC，AE的延长线交BC于D，则图中全等的三角形共有_____对．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△EBD中，EB=ED,点C在BD上，CE=CD，BE⊥CE，A是CE延长线上一点，EA=EC.

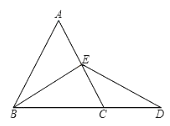
    （1）求∠EBC的度数；

    （2）求证△ABC为等边三角形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等边△ABC中，点D在BC边上，点E在AC的延长线上，DE＝DA．

    (1)求证：∠BAD＝∠EDC；

    (2)作出点E关于直线BC的对称点M，连接DM、AM，猜想DM与AM的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，将任意两点P（x1，y1）与Q（x2，y2）之间的“直距”定义为：DPQ=|x1﹣x2|+|y1﹣y2|．

    例如：点M（1，﹣2），点N（3，﹣5），则DMN=|1﹣3|+|﹣2﹣（﹣5）|=5．已知点A（1，0）、点B（﹣1，4）．

    （1）则DAO=　　，DBO=　　；

    （2）如果直线AB上存在点C，使得DCO为2，请你求出点C的坐标；

    （3）如果⊙B的半径为3，点E为⊙B上一点，请你直接写出DEO的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算:学习了分式运算后，老师布置了这样一道计算题：，甲、乙两位同学的解答过程分别如下：

    甲同学：

    ①

    ②

    ③

    ④

    乙同学：

    ①

    ②

    ③

    ④

    老师发现这两位同学的解答过程都有错误.

    请你从甲、乙两位同学中，选择一位同学的解答过程，帮助他分析错因，并加以改正.

    （1）我选择________同学的解答过程进行分析. （填“甲”或“乙”）

    （2）该同学的解答从第________步开始出现错误（填序号），错误的原因是________；

    （3）请写出正确解答过程.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

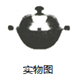
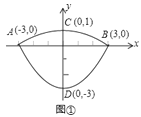
    【题目】我们常见的炒菜锅和锅盖都是抛物线面，经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形，不妨简称为“锅线”，锅口直径为，锅深，锅盖高（锅口直径与锅盖直径视为相同），建立直角坐标系如图①所示（图②是备用图），如果把锅纵断面的抛物线记为，把锅盖纵断面的抛物线记为．

    求和的解析式；

    如果炒菜锅时的水位高度是，求此时水面的直径；

    如果将一个底面直径为，高度为的圆柱形器皿放入炒菜锅内蒸食物，锅盖能否正常盖上？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB∥CD，CE、BE的交点为E，现作如下操作：

    第一次操作，分别作∠ABE和∠DCE的平分线，交点为E1，

    第二次操作，分别作∠ABE1和∠DCE1的平分线，交点为E2，

    第三次操作，分别作∠ABE2和∠DCE2的平分线，交点为E3，…，

    第n次操作，分别作∠ABEn﹣1和∠DCEn﹣1的平分线，交点为En．

    若∠En=1度，那∠BEC等于　 　度

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在等边中，点D、E分别在边BC、AB上，且，AD与CE交于点F，则的度数为　　

    A.B.C.D.

    查看答案和解析>>

    同步练习册答案