
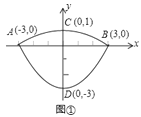
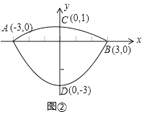
����Ŀ�����dz����ij��˹����Ƕ����������棬�������ĺ��ĵ��ݶ�����������������϶��ɵķ��ͼ�Σ��������Ϊ��������������ֱ��Ϊ![]() ������
������![]() �����Ǹ�
�����Ǹ�![]() ������ֱ�������ֱ����Ϊ��ͬ��������ֱ������ϵ��ͼ����ʾ��ͼ���DZ���ͼ��������ѹ��ݶ����������Ϊ
������ֱ�������ֱ����Ϊ��ͬ��������ֱ������ϵ��ͼ����ʾ��ͼ���DZ���ͼ��������ѹ��ݶ����������Ϊ![]() ���ѹ����ݶ����������Ϊ
���ѹ����ݶ����������Ϊ![]() ��
��
![]() ��
��![]() ��
��![]() �Ľ���ʽ��
�Ľ���ʽ��
![]() ������˹�ʱ��ˮλ�߶���
������˹�ʱ��ˮλ�߶���![]() �����ʱˮ���ֱ����
�����ʱˮ���ֱ����
![]() �����һ������ֱ��Ϊ
�����һ������ֱ��Ϊ![]() ���߶�Ϊ
���߶�Ϊ![]() ��Բ����������보�˹�����ʳ������ܷ��������ϣ���˵�����ɣ�
��Բ����������보�˹�����ʳ������ܷ��������ϣ���˵�����ɣ�
���𰸡�![]()
![]() ��
��![]() ��
��![]() ��ʱˮ���ֱ��Ϊ
��ʱˮ���ֱ��Ϊ![]() ��
��![]() �������������ϣ����ɼ�����.
�������������ϣ����ɼ�����.
��������
��1����֪A��B��C��D�ĵ����꣬���ô���ϵ��������ȷ���������Ľ���ʽ��
��2�����˹����ˮλ�߶�Ϊ1dm��y=-2���з������x��ֵ���ɵô𰸣�
��3������ֱ��Ϊ3dm���߶�Ϊ3dmԲ���������ܷ������ڣ����жϵ�![]() ʱ��C1��C2�е�yֵ�IJ���3�Ƚϴ�С���Ӷ��ɵô𰸣�
ʱ��C1��C2�е�yֵ�IJ���3�Ƚϴ�С���Ӷ��ɵô𰸣�
![]() ����������
����������![]() ��
��![]() ������
������![]() ��
��![]() ���������ǵĽ���ʽΪ��
���������ǵĽ���ʽΪ��![]() ��
��
������![]() ������
������![]() ��
��
���У�![]() ����ã�
����ã�![]()
����������![]() ��
��
������![]() ������
������![]() ��
��
���У�![]() ����ã�
����ã�![]()
����������![]() ��
��
![]() �����˹����ˮλ�߶�Ϊ
�����˹����ˮλ�߶�Ϊ![]() ʱ��
ʱ��![]() ����
����![]() ��
��
��ã�![]() ��
��
���ʱˮ���ֱ��Ϊ![]() ��
��
![]() �������������ϣ��������£�
�������������ϣ��������£�
��![]() ʱ��������
ʱ��������![]() ��������
��������![]() ��
��
��![]() ��
��
��������������ϣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ѧ��ȤС���ڻ���ϲ���ѧУ��˵ĸ߶ȣ���֪С��վ�Ų������۾������ľ��루AB����1.7�ף�����˶���E������Ϊ30����С�����Ų������۾������ľ��루CD����0.7�ף�����˶���E������Ϊ45�����������5����λ�����ͬ�ࣨ��B��D��F��ͬһֱ���ϣ���
��1����С������˵ľ���DF��������������ţ�
��2�������EF�ĸ߶ȣ�����������������ο����ݣ�![]() ��1.4��
��1.4��![]() ��1.7��
��1.7��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ƶ�ͨѶ��˾�������ƶ��绰�Ʒѷ�ʽ�������ּƷѷ�ʽ����ʹ�÷�y��Ԫ��������ʱ��x���֣��Ķ�Ӧ��ϵ��ͼ��ʾ��������ʱ�䲻��1���ӣ���1�����շѣ����������ж�����ȷ���ǣ�������
�ٷ�ʽһÿ������ʱ��Ϊ300����ʱ����ʹ�÷�Ϊ88Ԫ
��ÿ������ʱ��Ϊ350���Ӻ�600����ʱ�����ַ�ʽ�շ���ͬ
��ÿ������ʱ�䳬��600���ӣ�ѡ��ʽһ��ʡǮ

A. �٢� B. �٢� C. �ڢ� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() �ױ�
�ױ�![]() �ij�Ϊ
�ij�Ϊ![]() �������
�������![]() ����
����![]() �Ĵ�ֱƽ����
�Ĵ�ֱƽ����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊ
Ϊ![]() ���ϵ��е㣬
���ϵ��е㣬![]() Ϊ�߶�
Ϊ�߶�![]() ��һ���㣬��
��һ���㣬��![]() ���ܳ�����СֵΪ�� ��
���ܳ�����СֵΪ�� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ����
�Ӽ��е����г�������·��Ϊ150ǧ�ף�������ͨ�г���·��Ϊ250ǧ�ס�������ƽ���ٶ�����ͨ�г�ƽ���ٶȵ�3���������ij˳�ʱ�����ͨ�г��ij˳�ʱ��������2Сʱ��������ƽ���ٶ���ÿСʱ����ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���A=36�㣬AC=AB=2������ABC�Ƶ�B��ʱ�뷽����ת�õ���DBE��ʹ��E�ڱ�AC�ϣ�DE��AB�ڵ�F������AFE����DBF�����֮�ȵ��ڣ�������
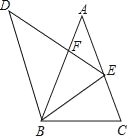
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǹ涨������������ָ���ݵ�����![]() ��a>0��m��n������������n.>1����
��a>0��m��n������������n.>1����![]() �����ǣ�������a>0��m��n������������n.>1�£���ʽ������д�ɷ���ָ���ݵ���ʽ�������ĸ�����ָ���ݵ������븺����ָ���ݵ�������£����ǹ涨
�����ǣ�������a>0��m��n������������n.>1�£���ʽ������д�ɷ���ָ���ݵ���ʽ�������ĸ�����ָ���ݵ������븺����ָ���ݵ�������£����ǹ涨
![]() ���涨�˷���ָ���ݵ������Ժ�ָ���ĸ���ʹ�����ָ���ƹ㵽��������ָ��������ָ���ݵ��������ʶ���������ָ����Ҳͬ�������������������壬�����������⣺
���涨�˷���ָ���ݵ������Ժ�ָ���ĸ���ʹ�����ָ���ƹ㵽��������ָ��������ָ���ݵ��������ʶ���������ָ����Ҳͬ�������������������壬�����������⣺
(1)��ֵ��![]() =____�� _____=
=____�� _____=![]() ��
��
(2)���㣺![]() _____��
_____��
(3)�÷���ָ���ݵ���ʽ����![]()
(4)![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��l��y=![]() x+m��x�ᡢy��ֱ��ڵ�A�͵�B��0����1����������y=
x+m��x�ᡢy��ֱ��ڵ�A�͵�B��0����1����������y=![]() x2+bx+c������B����ֱ��l����һ������ΪC��4��n����
x2+bx+c������B����ֱ��l����һ������ΪC��4��n����
��1����n��ֵ�������ߵĽ���ʽ��
��2����D���������ϣ�DE��y�ύֱ��l�ڵ�E����F��ֱ��l�ϣ����ı���DFEGΪ���Σ���ͼ2�������D�ĺ�����Ϊt��0��t��4��������DFEG���ܳ�Ϊp����p��t�ĺ�����ϵʽ�Լ�p�����ֵ��
��3������AOB��ƽ����ij��M��ת90���180�㣬�õ���A1O1B1����A��O��B�Ķ�Ӧ��ֱ��ǵ�A1��O1��B1������A1O1B1����������ǡ�������������ϣ���ô���Ǿͳ������ĵ�Ϊ����㡱����ֱ��д������㡱�ĸ�������ת180��ʱ��A1�ĺ����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ŀڴ���װ���ĸ��ֱ����1��2��3��4��С�����ǵ���״����С����ȫ��ͬ��С���ȴӿڴ���������Żص�ȡ��һ��С��������Ϊx��С����ʣ��������С�������ȡ��һ��С��������y��
��1��������x��yȷ���ĵ㣨x��y���ں���y=��x+6ͼ���ϵĸ��ʣ�
��2��С����С��Լ����һ����Ϸ��������ǣ���x��y����xy��6����С��ʤ����x��y����xy��6����С��ʤ�������Ϸ����ƽ��˵�����ɣ�������ƽ����������Ϸ����Ŷ�˫����ƽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com