
【题目】某移动通讯公司有两种移动电话计费方式,这两种计费方式中月使用费y(元)与主叫时间x(分)的对应关系如图所示:(主叫时间不到1分钟,按1分钟收费)下列三个判断中正确的是( )
①方式一每月主叫时间为300分钟时,月使用费为88元
②每月主叫时间为350分钟和600分钟时,两种方式收费相同
③每月主叫时间超过600分钟,选择方式一更省钱

A. ①② B. ①③ C. ②③ D. ①②③
【答案】C
【解析】
①根据待定系数法求出方式一,当x≥200时的一次函数解析式,再求出y=88时x的值即可求解;
②得出两交点坐标即可求解;
③观察函数图形即可求解.
①当x≥200时,设方式一的一次函数解析式为y=kx+b,依题意有,
![]() ,
,
解得![]() .
.
则当x≥200时,方式一的一次函数解析式为y=0.2x+18,
当y=88时,0.2x+18=88,解得x=350.
故方式一每月主叫时间为350分钟时,月使用费为88元.题干原来的说法是错误的;
②观察图形可知两交点坐标分别是(350,88),(600,138),
故每月主叫时间为350分钟和600分钟时,两种方式收费相同.题干原来的说法是正确的;
③观察图形可知每月主叫时间超过600分钟,选择方式一更省钱.题干原来的说法是正确的.
故选C.


科目:初中数学 来源: 题型:
【题目】江苏省锡中实验学校为了解九年级学生的身体素质测试情况,随机抽取了该市九年级部分学生的身体素质测试成绩作为样本,按A(优秀),B(良好),C(合格),D(不合格)四个等级进行统计,并将统计结果绘制了如图两幅不完整的统计图,请根据图中提供的信息,解答下列问题:

(1)此次共调查了多少名学生;
(2)将条形统计图补充完整,并计算扇形统计图中“A”部分所对应的圆心角的度数;
(3)该市九年级共有1000名学生参加了身体素质测试,估计测试成绩在良好以上(含良好)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 的中点,点
的中点,点![]() 在射线
在射线![]() 上,点
上,点![]() 在射线
在射线![]() 上,
上,![]() .
.
(1)如图1,若点![]() 与
与![]() 点重合,求证:
点重合,求证:![]() ;
;

(2)如图2,若点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,求
上,求![]() 的值;
的值;

(3)如图3,若![]() ,直接写出
,直接写出![]() 的度数为______.
的度数为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△EBD中,EB=ED,点C在BD上,CE=CD,BE⊥CE,A是CE延长线上一点,EA=EC.
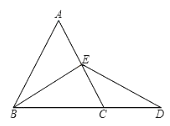
(1)求∠EBC的度数;
(2)求证△ABC为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
(1)求该抛物线的解析式及顶点M的坐标;
(2)求△EMF与△BNF的面积之比.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA.
(1)求证:∠BAD=∠EDC;
(2)作出点E关于直线BC的对称点M,连接DM、AM,猜想DM与AM的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将任意两点P(x1,y1)与Q(x2,y2)之间的“直距”定义为:DPQ=|x1﹣x2|+|y1﹣y2|.
例如:点M(1,﹣2),点N(3,﹣5),则DMN=|1﹣3|+|﹣2﹣(﹣5)|=5.已知点A(1,0)、点B(﹣1,4).
(1)则DAO= ,DBO= ;
(2)如果直线AB上存在点C,使得DCO为2,请你求出点C的坐标;
(3)如果⊙B的半径为3,点E为⊙B上一点,请你直接写出DEO的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为![]() ,锅深
,锅深![]() ,锅盖高
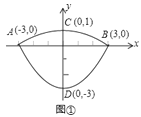
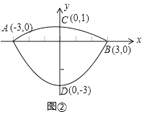
,锅盖高![]() (锅口直径与锅盖直径视为相同),建立直角坐标系如图①所示(图②是备用图),如果把锅纵断面的抛物线记为
(锅口直径与锅盖直径视为相同),建立直角坐标系如图①所示(图②是备用图),如果把锅纵断面的抛物线记为![]() ,把锅盖纵断面的抛物线记为
,把锅盖纵断面的抛物线记为![]() .
.
![]() 求
求![]() 和
和![]() 的解析式;
的解析式;
![]() 如果炒菜锅时的水位高度是
如果炒菜锅时的水位高度是![]() ,求此时水面的直径;
,求此时水面的直径;
![]() 如果将一个底面直径为
如果将一个底面直径为![]() ,高度为
,高度为![]() 的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面内有一等腰Rt△ABC,∠ACB=90°,点A在直线l上.过点C作CE⊥1于点E,过点B作BF⊥l于点F,测量得CE=3,BF=2,则AF的长为( )

A. 5 B. 4 C. 8 D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com