
【题目】已知![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 的中点,点
的中点,点![]() 在射线
在射线![]() 上,点
上,点![]() 在射线
在射线![]() 上,
上,![]() .
.
(1)如图1,若点![]() 与
与![]() 点重合,求证:
点重合,求证:![]() ;
;

(2)如图2,若点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,求
上,求![]() 的值;
的值;

(3)如图3,若![]() ,直接写出
,直接写出![]() 的度数为______.
的度数为______.

【答案】(1)见详解;(2)![]() ;(3)15°.
;(3)15°.
【解析】
(1)由△ABC是等边三角形,则BD是高也是角平分线,则∠DBC=30°,∠BDC=90°,由![]() ,可求∠CDE=∠E=30°,即可得到DB=DE;
,可求∠CDE=∠E=30°,即可得到DB=DE;
(2)过点D作DG⊥BC,DH⊥AB,连接BD,由∠ABC=60°,得到∠GDH=120°=∠EDF,得到∠FDH=∠EDG,又BD平分∠ABC,则DH=DG,可证△FDH≌△EDG,得到FH=EG,则BE+BF=BH+BG=2BG,设AC=BC=2k,则CD=k,CG=![]() ,得到BG=
,得到BG=![]() ,即可得到
,即可得到![]() 的值.
的值.
(3)如图,在BC上截取CM=AF,连接DM,DF,DE,由![]() ,则
,则![]() ,先证明△AFD≌△CMD,得到DF=DM,由(2)知DF=DE,则DM=DE,则△MED是等腰三角形,则MG=EG=
,先证明△AFD≌△CMD,得到DF=DM,由(2)知DF=DE,则DM=DE,则△MED是等腰三角形,则MG=EG=![]() ,设AC=2k,则ME=BD=
,设AC=2k,则ME=BD=![]() ,则DG=
,则DG=![]() ,则△EDG是等腰直角三角形,得∠E=45°,即可得到∠EDC=15°.
,则△EDG是等腰直角三角形,得∠E=45°,即可得到∠EDC=15°.
(1)证明:如图,
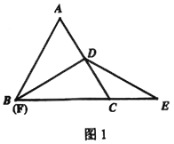
∵△ABC是等边三角形,D是AC中点,
∴AC⊥BD,BD平分∠ABC,
∴∠DBC=30°,∠BDC=90°,
∵![]() ,
,
∴∠CDE=30°,
∵∠ACB=60°,
∴∠E=30°=∠DBC,
∴BD=ED;
(2)解:如图,过点D作DG⊥BC,DH⊥AB,连接BD,则∠BHD=∠BGD=90°,
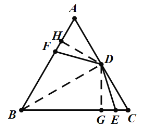
∵∠ABC=60°,
∴∠GDH=120°=∠EDF,
∴∠FDH=∠EDG,
∵BD平分∠ABC,
∴DH=DG,
∴△FDH≌△EDG,
∴FH=EG,
∵BH=BG,
∴BE+BF=BH+BG=2BG,
∠CBD=∠CDG=30°,
设AC=BC=2k,∠CBD=∠CDG=30°,
∴CD=k,CG=![]() ,
,
∴BG=![]() ,DG=
,DG=![]() ,
,
∴![]() ;
;
(3)如图,在BC上截取CM=AF,连接DM,DF,DE,
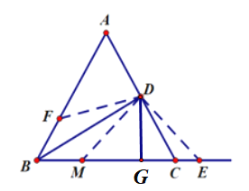
∵![]() ,
,
∴![]() ,
,
∵AD=CD,∠A=∠ACD,
∴△AFD≌△CMD,
∴DF=DM,
由(2)知DF=DE,
∴DM=DE,
∴△MED是等腰三角形,
∴MG=EG=![]() ,
,
由(2)设AC=2k,则ME=BD=![]() ,
,
∴DG=![]() ,
,
∴△EDG是等腰直角三角形,
∴∠E=45°,
∵∠ACB=60°,
∴∠EDC=![]() .
.
故答案为:15°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在ΔABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D点,
交AC于点E.
(1)若∠ABE=38°,求∠EBC的度数;
(2)若ΔABC的周长为36cm,一边为13cm,求ΔBCE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c).
(1)用这样的两个三角形构造成如图(2)的图形(B,E,C三点在一条直线上),利用这个图形,求证:a2+b2=c2
(2)当a=1,b=2时,将其中一个直角三角形放入平面直角坐标系中(如图(3)),使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合.
请在坐标轴上找一点C,使△ABC为等腰三角形.
写出一个满足条件的在x轴上的点的坐标: ;
写出一个满足条件的在y轴上的点的坐标: ,这样的点有 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).
(1)求小敏到旗杆的距离DF.(结果保留根号)
(2)求旗杆EF的高度.(结果保留整数,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边(
表示直角三角形的两直角边(![]() ),下列四个说法:
),下列四个说法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BC=4,△ABC的面积是16,AC边的垂直平分线EF分别交AC,AB边于点E,F. 若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为()
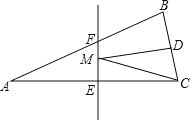
A.4B.5C.10D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某移动通讯公司有两种移动电话计费方式,这两种计费方式中月使用费y(元)与主叫时间x(分)的对应关系如图所示:(主叫时间不到1分钟,按1分钟收费)下列三个判断中正确的是( )
①方式一每月主叫时间为300分钟时,月使用费为88元
②每月主叫时间为350分钟和600分钟时,两种方式收费相同
③每月主叫时间超过600分钟,选择方式一更省钱

A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定正数的正分数指数幂的意义![]() (a>0,m,n是正整数,且n.>1)如
(a>0,m,n是正整数,且n.>1)如![]() .于是,在条件a>0,m,n是正整数,且n.>1下,根式都可以写成分数指数幂的形式.正数的负分数指数幂的意义与负整数指数幂的意义相仿,我们规定
.于是,在条件a>0,m,n是正整数,且n.>1下,根式都可以写成分数指数幂的形式.正数的负分数指数幂的意义与负整数指数幂的意义相仿,我们规定
![]() ,规定了分数指数幂的意义以后,指数的概念就从整数指数推广到了有理数指数.整数指数幂的运算性质对于有理数指数幂也同样适用.根据上述定义,解答下面的问题:
,规定了分数指数幂的意义以后,指数的概念就从整数指数推广到了有理数指数.整数指数幂的运算性质对于有理数指数幂也同样适用.根据上述定义,解答下面的问题:
(1)求值:![]() =____, _____=
=____, _____=![]() ;
;
(2)计算:![]() _____;
_____;
(3)用分数指数幂的形式表:![]()
(4)![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com