
【题目】如图,在平面内有一等腰Rt△ABC,∠ACB=90°,点A在直线l上.过点C作CE⊥1于点E,过点B作BF⊥l于点F,测量得CE=3,BF=2,则AF的长为( )

A. 5 B. 4 C. 8 D. 7
【答案】B
【解析】
过点C作CD⊥BF,交FB的延长线于点D,易证△ACE≌△BCD,根据全等三角形的对应边相等,即可证得AF+BF=2CE,由此即可解决问题。
(1)证明:如图1,过点C作CD⊥BF,交FB的延长线于点D,
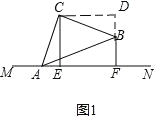
∵CE⊥MN,CD⊥BF,
∴∠CEA=∠D=90°,
∵CE⊥MN,CD⊥BF,BF⊥MN,
∴四边形CEFD为矩形,
∴∠ECD=90°,
又∵∠ACB=90°,
∴∠ACB-∠ECB=∠ECD-∠ECB,
即∠ACE=∠BCD,
又∵△ABC为等腰直角三角形,
∴AC=BC,
在△ACE和△BCD中,
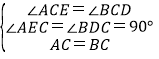 ,
,
∴△ACE≌△BCD(AAS),
∴AE=BD,CE=CD,
又∵四边形CEFD为矩形,
∴四边形CEFD为正方形,
∴CE=EF=DF=CD,
∴AF+BF=AE+EF+BF
=BD+EF+BF
=DF+EF
=2CE,
∵CE=3,BF=2,
∴AF=6-2=4.
故选B.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】一本小说共![]() 页,一位同学第一天看了全书的
页,一位同学第一天看了全书的![]() 少6页,第二天看了剩下的
少6页,第二天看了剩下的![]() 多6页,第三天把剩下的全部看完.
多6页,第三天把剩下的全部看完.
①该同学第一天看了多少页?
②该同学第二天看了多少页?
③若![]() ,则第三天看了多少页?
,则第三天看了多少页?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形![]() 与正方形(点C、E、F、G按顺时针排列),是的中点,连接,.
与正方形(点C、E、F、G按顺时针排列),是的中点,连接,.
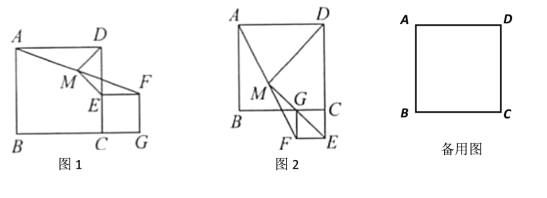
(1)如图1,点![]() 在上,点在的延长线上,
在上,点在的延长线上,
求证:![]() =ME,
=ME,![]() ⊥.ME
⊥.ME
简析: 由是的中点,AD∥EF,不妨延长EM交AD于点N,从而构造出一对全等的三角形,即 ≌ .由全等三角形性质,易证△DNE是 三角形,进而得出结论.
(2)如图2, 在![]() 的延长线上,点在上,(1)中结论是否成立?若成立,请证明你的结论;若不成立,请说明理由.
的延长线上,点在上,(1)中结论是否成立?若成立,请证明你的结论;若不成立,请说明理由.
(3)当AB=5,CE=3时,正方形的顶点C、E、F、G按顺时针排列.若点![]() 在直线CD上,则DM= ;若点E在直线BC上,则DM= .
在直线CD上,则DM= ;若点E在直线BC上,则DM= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走.
(1)假如每天能运x立方米,所需时间为y天,写出y与x之间的函数解析式(不要求写出自变量的取值范围);
(2)若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的条件下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
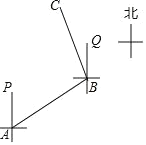
【题目】为全力推进农村公路快速发展,解决农村“出行难”问题,现将 A、B、C 三村连通的公路进行硬化改造(如图所示),铺设成水泥路面.已知 B 村在 A 村的北偏东 60°方向上,∠ABC=110°.
(1)C 村在 B 村的什么方向上?
(2)甲、乙两个施工队分别从 A 村、C 村向 B 村施工,两队的施工进度相同A 村到 B 村的距离比 C 到 B 村的距离多 400 米,甲队用了 9 天完成铺设任务乙队用了 7 天完成铺设任务,求两段公路的总长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,BC=8,作AD⊥BC于点D,AD=![]() AB,点E为AC边上的中点,点P为BC上一动点,则PA+PE的最小值为_____.
AB,点E为AC边上的中点,点P为BC上一动点,则PA+PE的最小值为_____.
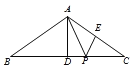
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BA=BE,∠A=∠E,∠ABE=∠CBD,ED交BC于点F,且∠FBD=∠D.
求证:AC∥BD.
证明:∵∠ABE=∠CBD(已知),
∴∠ABE+∠EBC=∠CBD+∠EBC( )
即∠ABC=∠EBD
在△ABC和△EBD中,
 ,
,
∴△ABC≌△EBD( ),
∴∠C=∠D( )
∵∠FBD=∠D,
∴∠C= (等量代换),
∴AC∥BD( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月25日,中国国际大数据产业博览会在贵阳会展中心开幕,博览会设了编号为1~6号展厅共6个,小雨一家计划利用两天时间参观其中两个展厅:第一天从6个展厅中随机选择一个,第二天从余下的5个展厅中再随机选择一个,且每个展厅被选中的机会均等.
(1)第一天,1号展厅没有被选中的概率是 ;
(2)利用列表或画树状图的方法求两天中4号展厅被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,设购进甲种花卉m盆,求当m的值等于40时,两种花卉全部销售后获得的利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com