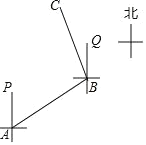
【题目】为全力推进农村公路快速发展，解决农村“出行难”问题，现将 A、B、C 三村连通的公路进行硬化改造(如图所示)，铺设成水泥路面．已知 B 村在 A 村的北偏东 60°方向上，∠ABC＝110°．
(1)C 村在 B 村的什么方向上？
(2)甲、乙两个施工队分别从 A 村、C 村向 B 村施工，两队的施工进度相同A 村到 B 村的距离比 C 到 B 村的距离多 400 米，甲队用了 9 天完成铺设任务乙队用了 7 天完成铺设任务，求两段公路的总长．
口算能手系列答案科目：初中数学 来源： 题型：
【题目】我们规定：有一组邻边相等,且这组邻边的夹角为
的凸四边形叫做“准筝形”。如图1,四边形ABCD中,若AB=AD,∠A=，则四边形ABCD是“准筝形”。
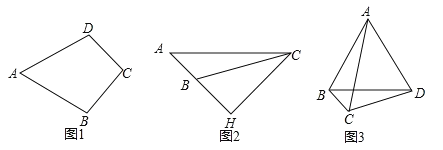
(1)如图2,CH是△ABC的高线,∠A=
,∠ABC=
，AB=2.求CH；
(2) 如图3,四边形ABCD中,BC=2,CD=4,AC=6,∠BCD=，且AD=BD，试判断四边形ABCD是不是“准筝形”，并说明理由。
小红是这样思考的：延长BC至点E，使CE=CD=4，连结DE，则△DCE是等边三角形，再说明△ACD
△BED就可以了。请根据小红的思考完成本小题。
(3) 在(1)条件下，设D是△ABC所在平面内一点，当四边形ABCD是“准筝形”时，请直接写出四边形ABCD的面积；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】今年秋季，斗门土特产喜获丰收，某土特产公司组织10辆汽车装运甲，乙，丙三种土特产去外地销售，按计划10辆车都要装运，每辆汽车只能装运同一士特产，且必须装满，设装运甲种士特产的汽车有x辆，装运乙种特产的汽车有y辆，根据下表提供的信息，解答以下问题：
土特产种类 | 甲 | 乙 | 丙 |
每辆汽车运载量（吨） | 4 | 3 | 6 |
每吨土特产获利（元） | 1000 | 900 | 1600 |
（1）装运丙种土特产的车辆数为 辆（用含有x，y的式子表示）；
（2）用含有x，y的式子表示这10辆汽车共装运土特产的数量；
（3）求销售完装运的这批土特产后所获得的总利润（用含有x，y的式子表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学组织学生到商场参加社会实践活动，他们参与了某种品牌运动鞋的销售工作，已知该运动鞋每双的进价为120元，为寻求合适的销售价格进行了4天的试销，试销情况如表所示：
（1）观察表中数据，x，y满足什么函数关系？请求出这个函数关系式；
（2）若商场计划每天的销售利润为3000元，则其单价应定为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面内有一等腰Rt△ABC，∠ACB=90°，点A在直线l上．过点C作CE⊥1于点E，过点B作BF⊥l于点F，测量得CE=3，BF=2，则AF的长为（ ）
A. 5 B. 4 C. 8 D. 7
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个不透明的盒子里装有红、黑两种颜色的球共60只，这些球除颜色外其余完全相同．为了估计红球和黑球的个数，七（4）班的数学学习小组做了摸球实验．他们]将球搅匀后，从盒子里随机摸出一个球记下颜色，再把球放回盒子中，多次重复上述过程，得到下表中的一组统计数据：
摸球的次数n | 50 | 100 | 300 | 500 | 800 | 1000 | 2000 |
摸到红球的次数m | 14 | 33 | 95 | 155 | 241 | 298 | 602 |
摸到红球的频率 | 0.28 | 0.33 | 0.317 | 0.31 | 0.301 | 0.298 | 0.301 |
（1）请估计：当次数n足够大时，摸到红球的频率将会接近 ；(精确到0.1)
（2）假如你去摸一次，则摸到红球的概率的估计值为 ；
（3）试估算盒子里红球的数量为 个，黑球的数量为 个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把长为22 cm的金属丝围成一个一条边长为x(cm)，面积为S(cm2)的矩形框．
(1)写出用x表示S的式子；
(2)在(1)中，若S＝10 cm2，请求出矩形的长和宽．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
