
【题目】我们规定:有一组邻边相等,且这组邻边的夹角为![]() 的凸四边形叫做“准筝形”。如图1,四边形ABCD中,若AB=AD,∠A=
的凸四边形叫做“准筝形”。如图1,四边形ABCD中,若AB=AD,∠A=![]() ,则四边形ABCD是“准筝形”。
,则四边形ABCD是“准筝形”。
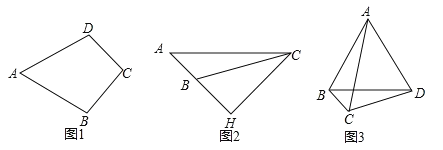
(1)如图2,CH是△ABC的高线,∠A=![]() ,∠ABC=
,∠ABC=![]() ,AB=2.求CH;
,AB=2.求CH;
(2) 如图3,四边形ABCD中,BC=2,CD=4,AC=6,∠BCD=![]() ,且AD=BD,试判断四边形ABCD是不是“准筝形”,并说明理由。
,且AD=BD,试判断四边形ABCD是不是“准筝形”,并说明理由。
小红是这样思考的:延长BC至点E,使CE=CD=4,连结DE,则△DCE是等边三角形,再说明△ACD![]() △BED就可以了。请根据小红的思考完成本小题。
△BED就可以了。请根据小红的思考完成本小题。
(3) 在(1)条件下,设D是△ABC所在平面内一点,当四边形ABCD是“准筝形”时,请直接写出四边形ABCD的面积;
【答案】(1)![]() (2)四边形ABCD是“准筝形”,理由见解析;(3)
(2)四边形ABCD是“准筝形”,理由见解析;(3)![]()
【解析】
(1)设BH=x,根据∠ABC=![]() 表示出CH,在根据∠A=
表示出CH,在根据∠A=![]() 列出方程求解即可;(2)延长BC至点E,使CE=CD=4,连结DE,则△DCE是等边三角形,再证明△ACD≌△BED得到△ABD是等边三角形,即可证明四边形ABCD是“准筝形”;(3)在(1)条件下,D是△ABC所在平面内一点,当四边形ABCD是“准筝形”时,分情况讨论①AB=AD=2,∠BAD=60°,②BC=BD=2
列出方程求解即可;(2)延长BC至点E,使CE=CD=4,连结DE,则△DCE是等边三角形,再证明△ACD≌△BED得到△ABD是等边三角形,即可证明四边形ABCD是“准筝形”;(3)在(1)条件下,D是△ABC所在平面内一点,当四边形ABCD是“准筝形”时,分情况讨论①AB=AD=2,∠BAD=60°,②BC=BD=2![]() +2,∠BCD=60°,③AD=CD=AC=
+2,∠BCD=60°,③AD=CD=AC=![]() HC=3
HC=3![]() +
+![]() ,∠ADC=60°,分别求出四边形ABCD的面积即可.
,∠ADC=60°,分别求出四边形ABCD的面积即可.
(1)设BH=x,
∵∠ABC=120°,CH是△ABC的高线,
∴∠BCH=30°,
∴HC=![]() ,
,
∵∠A=45°,
∴HA=HC,
∵AB=2,
∴![]() =2+x,
=2+x,
解得:x=![]() +1,
+1,
∴HC=![]() =3+
=3+![]() ;
;
(2)四边形ABCD是“准筝形”,
理由:如图所示,延长BC至点E,使CE=CD=4,连结DE,
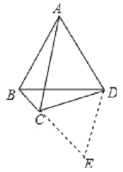
∵∠BCD=120°,
∴∠DCE=60°,
∴△DCE是等边三角形,
∴ED=CD=4,∠CDE=60°,
∵BC=2,CE=CD=4,AC=6,
∴AC=EB,
在△ACD和△BED中,
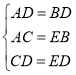
∴△ACD≌△BED(SSS),
∴∠ADC=∠BDE,
∴∠ADB=∠CDE=60°,
∴△ABD是等边三角形,
∴AB=AD,∠BAD=60°,
∴四边形ABCD是“准筝形”;
(3在(1)条件下,D是△ABC所在平面内一点,当四边形ABCD是“准筝形”时,分情况讨论,分别求出四边形ABCD的面积:
①如下图AB=AD=2,∠BAD=60°,
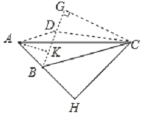
作CG垂直BD的延长线于点G,则BD=2,
易得:∠CBG=60°=∠CBH,
在△CBG和△CBH中
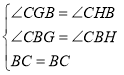
∴△CBG≌△CBH(AAS),
∴GC=HC=3+![]() ,
,
作AK⊥BD于K,则易得:AK=![]() ,
,
∴S△ABD=![]() ×2×
×2×![]() =
=![]() ,S△CBD=
,S△CBD=![]() ×2×(3+
×2×(3+![]() )=3+
)=3+![]() ,
,
∴四边形ABCD的面积=3+2![]() ;
;
②如下图BC=BD=2![]() +2,∠BCD=60°,
+2,∠BCD=60°,
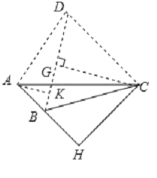
作CG垂直BD的延长线于点G,则BD=2![]() +2,
+2,
易得:CG=3+![]() ,AK=
,AK=![]() ,
,
∴S△BCD=![]() ×(3+
×(3+![]() )(2+2
)(2+2![]() )=4
)=4![]() +6,
+6,
S△ABD=![]() ×
×![]() ×(2+2
×(2+2![]() )=3+
)=3+![]() ,
,
∴四边形ABCD的面积=9+5![]() ;
;
③如下图AD=CD=AC=![]() HC=3
HC=3![]() +
+![]() ,∠ADC=60°,
,∠ADC=60°,
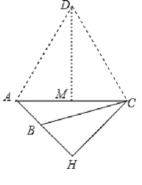
作DM⊥AC于M,
易得:DM=![]() (3
(3![]() +
+![]() )=
)=![]() (
(![]() +
+![]() ),
),
∴S△ABC=![]() ×2×(3+
×2×(3+![]() )=3+
)=3+![]() ,
,
S△ADC=![]() ×(3
×(3![]() +
+![]() )×
)×![]() (
(![]() +
+![]() )=6
)=6![]() +9,
+9,
∴四边形ABCD的面积=12+7![]() ,
,
综上所述,四边形ABCD的面积为![]()


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
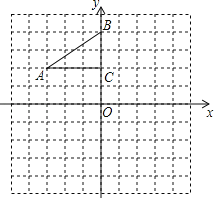
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(1,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
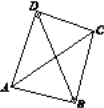
【题目】定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.
(1)如图,在损矩形ABCD中,∠ABC=∠ADC=90°,则该损矩形的直径是线段________.
(2)在损矩形ABCD内是否存在点O,使得A,B,C,D四个点都在以点O为圆心的同一个圆上?如果存在,请指出点O的具体位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 为边
为边![]() 上的一个动点,过点
上的一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的外角平分线
的外角平分线![]() 于点
于点![]() ,交
,交![]() 的角平分线
的角平分线![]() 于
于![]() .
.
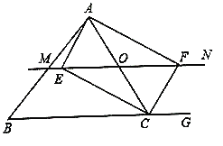
(1)求证:![]() ;
;
(2)当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?并证明你的结论;
是矩形?并证明你的结论;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一本小说共![]() 页,一位同学第一天看了全书的
页,一位同学第一天看了全书的![]() 少6页,第二天看了剩下的
少6页,第二天看了剩下的![]() 多6页,第三天把剩下的全部看完.
多6页,第三天把剩下的全部看完.
①该同学第一天看了多少页?
②该同学第二天看了多少页?
③若![]() ,则第三天看了多少页?
,则第三天看了多少页?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
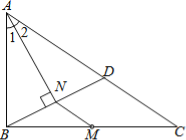
(1)求证:BN=DN;
(2)求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
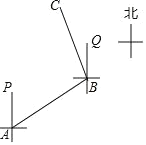
【题目】如图,一艘渔船位于港口A的北偏东60°方向,距离港口20海里的B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发,经过20分钟到达C处,求救援船的航行速度.(sin37°≈0.6,cos37°≈0.8,![]() ≈1.732,结果取整数)
≈1.732,结果取整数)
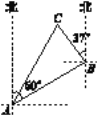
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为全力推进农村公路快速发展,解决农村“出行难”问题,现将 A、B、C 三村连通的公路进行硬化改造(如图所示),铺设成水泥路面.已知 B 村在 A 村的北偏东 60°方向上,∠ABC=110°.
(1)C 村在 B 村的什么方向上?
(2)甲、乙两个施工队分别从 A 村、C 村向 B 村施工,两队的施工进度相同A 村到 B 村的距离比 C 到 B 村的距离多 400 米,甲队用了 9 天完成铺设任务乙队用了 7 天完成铺设任务,求两段公路的总长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com