【题目】定义：只有一组对角是直角的四边形叫做损矩形，连接它的两个非直角顶点的线段叫做这个损矩形的直径．
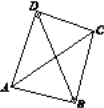
(1)如图，在损矩形ABCD中，∠ABC＝∠ADC＝90°，则该损矩形的直径是线段________．
(2)在损矩形ABCD内是否存在点O，使得A，B，C，D四个点都在以点O为圆心的同一个圆上？如果存在，请指出点O的具体位置．
科学实验活动册系列答案科目：初中数学 来源： 题型：
【题目】下列各选项中所列举的两个变量之间的关系，是反比例函数关系的是( )
A. 直角三角形中，30°角所对的直角边长y与斜边长x之间的关系
B. 等腰三角形中顶角与底角之间的关系
C. 圆的面积S与它的直径d之间的关系
D. 面积为20 cm2的菱形，其中一条对角线长y与另一条对角线长x之间的关系
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AB＝4，BC＝3，点Q在BC上，BQ＝2，点P是AB上的一个动点，连接PQ，将△PBQ沿PQ翻折，点B落在点B′．
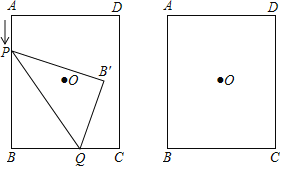
（1）当AP＝ 时，四边形PBQB′的面积是矩形面积的
；
（2）当AP为何值时，四边形PBQB′是正方形？为什么？
（3）在翻折过程中是否存在AP的值，使得点B′与矩形对称中心点O重合，如果存在，请求出AP的值；如果不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义一种对正整数n的“F”运算：①当n为奇数时，F（n）＝3n+1；②当n为偶数时，F（n）＝
（其中k是使F（n）为奇数的正整数）……，两种运算交替重复进行，例如，取n＝24，则：若n＝13，则第2018次“F”运算的结果是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，点C在线段AB上，AC = 8 cm，CB = 6 cm，点M、N分别是AC、BC的中点.
（1）求线段MN的长.
（2）若C为线段AB上任意一点，满足AC+CB=a(cm)，其他条件不变，你能猜想出MN的长度吗？并说明理由.
（3）若C在线段AB的延长线上，且满足AC-CB=b(cm)，M、N分别为AC、BC的中点，你能猜想出MN的长度吗？请画出图形，写出你的结论，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于实数a、b,定义一种运算“U”为：aUb=a2+ab-2,有下列命题：
①1U3=2； ②方程xU1=0的根为：x1=-2，x2=1；
③不等式组
的解集为：-1＜x＜4；
其中正确的是（ ）
A. ①②③；B. ①③；C. ①②；D. ②③．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们规定：有一组邻边相等,且这组邻边的夹角为
的凸四边形叫做“准筝形”。如图1,四边形ABCD中,若AB=AD,∠A=，则四边形ABCD是“准筝形”。
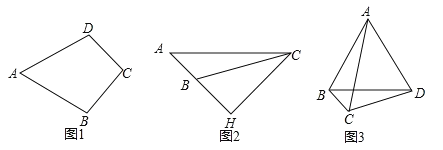
(1)如图2,CH是△ABC的高线,∠A=
,∠ABC=
，AB=2.求CH；
(2) 如图3,四边形ABCD中,BC=2,CD=4,AC=6,∠BCD=，且AD=BD，试判断四边形ABCD是不是“准筝形”，并说明理由。
小红是这样思考的：延长BC至点E，使CE=CD=4，连结DE，则△DCE是等边三角形，再说明△ACD
△BED就可以了。请根据小红的思考完成本小题。
(3) 在(1)条件下，设D是△ABC所在平面内一点，当四边形ABCD是“准筝形”时，请直接写出四边形ABCD的面积；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】今年秋季，斗门土特产喜获丰收，某土特产公司组织10辆汽车装运甲，乙，丙三种土特产去外地销售，按计划10辆车都要装运，每辆汽车只能装运同一士特产，且必须装满，设装运甲种士特产的汽车有x辆，装运乙种特产的汽车有y辆，根据下表提供的信息，解答以下问题：
土特产种类 | 甲 | 乙 | 丙 |
每辆汽车运载量（吨） | 4 | 3 | 6 |
每吨土特产获利（元） | 1000 | 900 | 1600 |
（1）装运丙种土特产的车辆数为 辆（用含有x，y的式子表示）；
（2）用含有x，y的式子表示这10辆汽车共装运土特产的数量；
（3）求销售完装运的这批土特产后所获得的总利润（用含有x，y的式子表示）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
