
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:若n=13,则第2018次“F”运算的结果是_____.
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:若n=13,则第2018次“F”运算的结果是_____.
![]()
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】点![]() 从数轴上表示+2的点开始移动,第1次向左移动1个单位,第2次向右移动2个单位;第3次向左移动3个单位,第4次向右移动4个单位;第5次向左移动5个单位……
从数轴上表示+2的点开始移动,第1次向左移动1个单位,第2次向右移动2个单位;第3次向左移动3个单位,第4次向右移动4个单位;第5次向左移动5个单位……
(1)写出第7次移动后这个点在数轴上表示的数为 ;
(2)直接写出第![]() 次移动后这个点在数轴上表示的数为 ;
次移动后这个点在数轴上表示的数为 ;
(3)如果第![]() 次移动后这个点在数轴上表示的数为56,求
次移动后这个点在数轴上表示的数为56,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数1至2019按照一定规律排成下表:
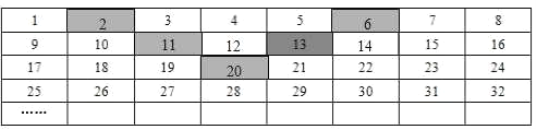
记![]() 表示第
表示第![]() 行第
行第![]() 个数,如
个数,如![]() 表示第1行第4个数是4.
表示第1行第4个数是4.
(1)直接写出![]() ,
,![]() ,
,![]() ;
;
(2)若![]() ,那么
,那么![]() ,
,![]()
(3)将表格中的5个阴影格子看成一个整体并平移,所覆盖的5个数之和能否等于2027? (填“能”或“不能”),若能,求出这5个数中的最小数,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
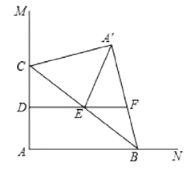
【题目】如图,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 为边
为边![]() 上一动点,连接
上一动点,连接![]() ,
,![]() 与
与![]() 关于
关于![]() 所在直线对称,点
所在直线对称,点![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,
为直角三角形时,![]() 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
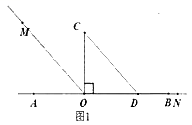
【题目】问题情境:以直线AB上一点O为端点作射线OM、ON,将一个直角三角形的直角顶点放在O处(∠COD=90°).
(1)如图1,直角三角板COD的边OD放在射线OB上,OM平分∠AOC,ON和OB重合,则∠MON=_°;
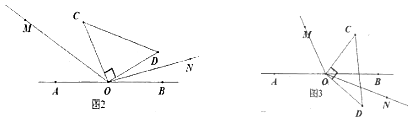
(2)直角三角板COD绕点O旋转到如图2的位置,OM平分∠AOC,ON平分∠BOD,求∠MON的度数。
(3)直角三角板COD绕点O旋转到如图3的位置,OM平分∠ AOC ,ON平分∠BOD,猜想∠MON的度数,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.
(1)如图,在损矩形ABCD中,∠ABC=∠ADC=90°,则该损矩形的直径是线段________.
(2)在损矩形ABCD内是否存在点O,使得A,B,C,D四个点都在以点O为圆心的同一个圆上?如果存在,请指出点O的具体位置.
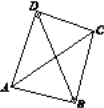
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
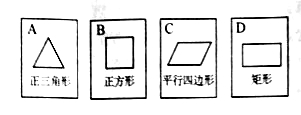
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 为边
为边![]() 上的一个动点,过点
上的一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的外角平分线
的外角平分线![]() 于点
于点![]() ,交
,交![]() 的角平分线
的角平分线![]() 于
于![]() .
.
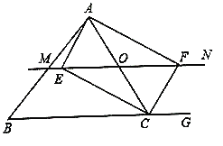
(1)求证:![]() ;
;
(2)当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?并证明你的结论;
是矩形?并证明你的结论;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:探究函数![]() 的图象与性质.
的图象与性质.
小明根据学习函数的经验,对函数![]() 的图象与性质进行了研究.
的图象与性质进行了研究.
下面是小明的研究过程,请补充完成.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … | -4 | -3 | -2 | -1 | 0 |
|
|
| 4 | … |
| … | 2 | 1 | 0 | n | 0 | 1 | m | 3 | 4 | … |
其中,m= n= ;
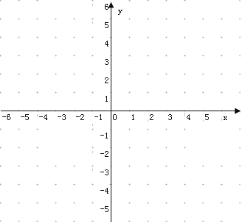
(2)在如图所示的平面直角坐标中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象.
(3)观察图象,写出该函数的两条性质.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com