
【题目】如图,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 为边
为边![]() 上一动点,连接
上一动点,连接![]() ,
,![]() 与
与![]() 关于
关于![]() 所在直线对称,点
所在直线对称,点![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,
为直角三角形时,![]() 的长为__________.
的长为__________.
【答案】4或![]()
【解析】
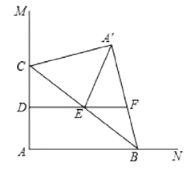
当△A'EF为直角三角形时,存在两种情况:①当∠A′EF=90°时,如图1,根据对称的性质和平行线可得:A′C=A′E=4,根据直角三角形斜边中线的性质得:BC=2A′B=8,最后利用勾股定理可得AB的长;
当∠A′FE=90°时,如图2,证明△ABC是等腰直角三角形,可得AB=AC=4.
当△A'EF为直角三角形时,存在两种情况:①当∠A′EF=90°时,如图1,
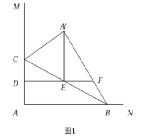
∵△A'BC与△ABC关于BC所在直线对称,
∴A′C=AC=4,∠ACB=∠A′CB,
∵点D,E分别为AC,BC的中点,
∴D、E是△ABC的中位线,
∴DE//AB,
∴∠CDE=∠MAN=90°,
∴∠CDE=∠A′EF,
∴AC//A′E,
∴∠ACB=∠A′EC,
∴∠A′CB=∠A′EC,
∴A′C=A′E=4,
Rt△A′CB中,∵E是斜边BC的中点,
∴BC=2A′E=8,
由勾股定理得:AB2=BC2AC2,
∴AB=![]() =
=![]() ;
;
②当∠A′FE=90°时,如图2,
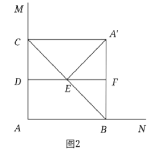
∵∠ADF=∠A=∠DFB=90°,
∴∠ABF=90°,
∵△A'BC与△ABC关于BC所在直线对称,
∴∠ABC=∠CBA′=45°,
∴△ABC是等腰直角三角形,
∴AB=AC=4;
综上所述,AB的长为![]() 或4;
或4;
故答案为:![]() 或4.
或4.


科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①绝对值等于本身的数是正数;②将数60340精确到千位是![]() ③连接两点的线段的长度就是两点间的距离;④若AC=BC,则点C就是线段AB的中点.
③连接两点的线段的长度就是两点间的距离;④若AC=BC,则点C就是线段AB的中点.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
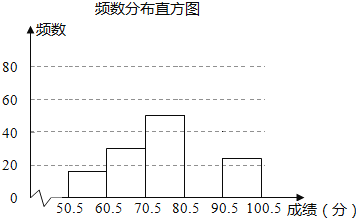
【题目】为弘扬中华传统文化,某校组织八年级800名学生参加汉字听写大赛为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,得到如下所示的模数分布表:
分数段 | 50.5﹣60.5 | 60.5﹣70.5 | 70.5﹣80.5 | 80.5﹣90.5 | 90.5﹣100.5 |
频数 | 16 | 30 | 50 | m | 24 |
所占百分比 | 8% | 15% | 25% | 40% | n |
请根据尚未完成的表格,解答下列问题:
(1)本次抽样调查的样本容量为 ,表中m= .n
(2)补全图中所示的频数分布直方图;
(3)若成绩超过80分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=3,点Q在BC上,BQ=2,点P是AB上的一个动点,连接PQ,将△PBQ沿PQ翻折,点B落在点B′.
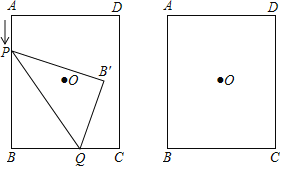
(1)当AP= 时,四边形PBQB′的面积是矩形面积的![]() ;
;
(2)当AP为何值时,四边形PBQB′是正方形?为什么?
(3)在翻折过程中是否存在AP的值,使得点B′与矩形对称中心点O重合,如果存在,请求出AP的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC=______度;
(2)求∠EDF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:若n=13,则第2018次“F”运算的结果是_____.
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:若n=13,则第2018次“F”运算的结果是_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a、b,定义一种运算“U”为:aUb=a2+ab-2,有下列命题:
①1U3=2; ②方程xU1=0的根为:x1=-2,x2=1;
③不等式组![]() 的解集为:-1<x<4;
的解集为:-1<x<4;
其中正确的是( )
A. ①②③;B. ①③;C. ①②;D. ②③.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知张强家、体育场、文具店在同一直线上.如图的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中x表示时间,y表示张强离家的距离.则下列说法错误的是( )
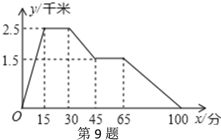
A. 体育场离张强家2.5千米
B. 体育场离文具店1千米
C. 张强在文具店逗留了15分钟
D. 张强从文具店回家的平均速度是![]() 千米/分
千米/分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com