
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC=______度;
(2)求∠EDF的度数.

【答案】(1)1100;(2)200
【解析】
(1)根据折叠的特点得出∠BAD=∠DAF,再根据三角形一个外角等于它不相邻两个内角之和,即可得出答案;
(2)根据已知求出∠ADB的值,再根据△ABD沿AD折叠得到△AED,得出∠ADE=∠ADB,最后根据∠EDF=∠EDA+∠BDA﹣∠BDF,即可得出答案.
解:(1)∵△ABD沿AD折叠得到△AED,
∴∠BAD=∠DAF,
∵∠B=50°∠BAD=30°,
∴∠AFC=∠B+∠BAD+∠DAF=110°;
故答案为110.
(2)∵∠B=50°,∠BAD=30°,
∴∠ADB=180°﹣50°﹣30°=100°,
∵△ABD沿AD折叠得到△AED,
∴∠ADE=∠ADB=100°,
∴∠EDF=∠EDA+∠BDA﹣∠BDF=100°+100°﹣180°=20°.


科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9,
(1)求证:△COD∽△CBE;
(2)求半圆O的半径的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A、1.5小时以上;B、1~1.5小时;C、0.5~1小时;D、0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,……按照此规律继续下去,则S2019的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在公路上行驶,看到里程表上是一个两位数,1小时后其里程表还是一个两位数,且刚好它的十位数字与个位数字与第一次看到的两位数的十位数字与个位数字颠倒了位置,又过了1小时后看到里程表是一个三位数,它是第一次看到的两位数中间加一个0,则汽车的速度是( )千米/小时.
A. 35B. 40C. 45D. 50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的对边,点
的对边,点![]() 是
是![]() 上一个动点(点
上一个动点(点![]() 与
与![]() 、
、![]() 不重合),连
不重合),连![]() ,若
,若![]() 、
、![]() 满足
满足![]() ,且
,且![]() 是不等式组
是不等式组 的最大整数解.
的最大整数解.
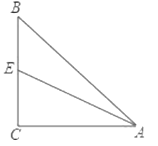
(1)求![]() ,
,![]() ,
,![]() 的长;
的长;
(2)若![]() 平分
平分![]() 的周长,求
的周长,求![]() 的大小;
的大小;
(3)是否存在线段![]() 将三角形
将三角形![]() 的周长和面积同时平分?若存在,求出
的周长和面积同时平分?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
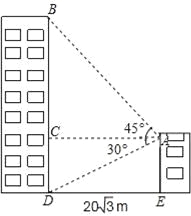
【题目】小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20![]() 米.
米.
(1)求出大厦的高度BD;
(2)求出小敏家的高度AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ ABCD中,E是AD边上一点,AD=4![]() ,CD=3,ED=
,CD=3,ED=![]() ,∠A=45.点P,Q分别是BC,CD边上的动点,且始终保持∠EPQ=45°.将
,∠A=45.点P,Q分别是BC,CD边上的动点,且始终保持∠EPQ=45°.将 ![]() CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,线段BP的长为________.
CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,线段BP的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA,OD是⊙O半径.过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B.
(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为 3cm,求![]() 的长度.(结果保留π)
的长度.(结果保留π)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com