【题目】一辆汽车在公路上行驶，看到里程表上是一个两位数，1小时后其里程表还是一个两位数，且刚好它的十位数字与个位数字与第一次看到的两位数的十位数字与个位数字颠倒了位置，又过了1小时后看到里程表是一个三位数，它是第一次看到的两位数中间加一个0，则汽车的速度是（ ）千米/小时.
A. 35B. 40C. 45D. 50
名校课堂系列答案科目：初中数学 来源： 题型：
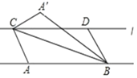
【题目】如图，已知直线
∥AB，与 AB 之间的距离为 2 ，C、D 是直线上
两个动点（点 C在 D 点的左侧），且 AB=CD=5．连接 AC、BC、BD，将△ABC 沿 BC 折叠得到△A′BC．若以 A′、C、B、D 为顶点的四边形为矩形，则此矩形相邻两边之和为____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某餐厅中，一张桌子可坐6人，有如图所示的两种摆放方式：
（1）当有n张桌子时，两种摆放方式各能坐多少人？
（2）一天中午餐厅要接待98位顾客共同就餐，但餐厅只有25张这样的餐桌.若你是这个餐厅的经理，你打算选择哪种方式来摆放餐桌？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
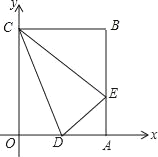
【题目】矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为（3，4），D是OA的中点，点E在AB上，当△CDE的周长最小时，点E的坐标为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
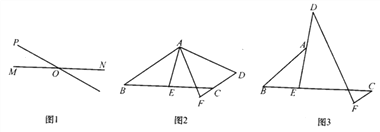
【题目】(l)操作：如图1，点O为线段MN的中点，直线PQ与MN相交于点O，请利用图1画出一对以点O为对称中心的全等三角形；根据上述操作得到的经验完成下列探究活动：
(2)探究一：如图2，在四边形ABCD中，AB∥DC,E为BC边的中点，∠BAE=∠EAF,AF与DC的延长线相交于点F．试探究线段AB与AF，AF,CF之间的等量关系，并证明你的结论；
(3)探究二：如图3 ,DE,BC相交于点E,BA交DE于点A，且BE：EC=1：2,∠BAE=∠EDF,CF∥AB．若AB=5，CF=1，求DF的长度.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，点D是BC边上的一点，∠B=50°，∠BAD=30°，将△ABD沿AD折叠得到△AED，AE与BC交于点F．
（1）填空：∠AFC=______度；
（2）求∠EDF的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
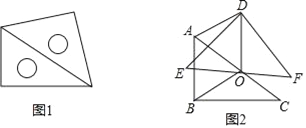
【题目】如图1，放置的一副三角尺，将含45°角的三角尺斜边中点O为旋转中心，逆时针旋转30°得到如图2，连接OB、OD、AD．
（1）求证：△AOB≌△AOD；
（2）试判定四边形ABOD是什么四边形，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，BC=2AB，对角线相交于O，过C点作CE⊥BD交BD于E点，H为BC中点，连接AH交BD于G点，交EC的延长线于F点，下列5个结论：①EH=AB；②∠ABG=∠HEC；③△ABG≌△HEC；④S△GAD=S四边形GHCE；⑤CF=BD．正确的有（ ）个．
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
