
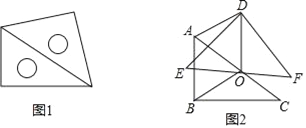
【题目】如图1,放置的一副三角尺,将含45°角的三角尺斜边中点O为旋转中心,逆时针旋转30°得到如图2,连接OB、OD、AD.
(1)求证:△AOB≌△AOD;
(2)试判定四边形ABOD是什么四边形,并说明理由.
【答案】(1)证明见解析;(2)四边形ABOD是菱形,理由见解析.
【解析】试题分析:(1)根据题意得:∠BAC=60°,∠ABC=∠EDF=90°,EF=AC,由直角三角形斜边上的中线性质得出OB=![]() AC=OA,OD=
AC=OA,OD=![]() EF=
EF=![]() AC=OB,由等腰三角形的性质得出OD⊥EF,证出△AOB是等边三角形,得出∠AOB=60°,由旋转的性质得:∠AOE=30°,证出∠AOD=60°,由SAS证明△AOB≌△AOD即可;
AC=OB,由等腰三角形的性质得出OD⊥EF,证出△AOB是等边三角形,得出∠AOB=60°,由旋转的性质得:∠AOE=30°,证出∠AOD=60°,由SAS证明△AOB≌△AOD即可;
(2)由全等三角形的性质得出AB=AD=OB=OD,即可得出四边形ABOD是菱形.
试题解析:(1)证明:根据题意得:∠BAC=60°,∠ABC=∠EDF=90°,EF=AC.
∵O为AC的中点,∴OB=![]() AC=OA,OD=
AC=OA,OD=![]() EF=
EF=![]() AC=OB,OD⊥EF,∴△AOB是等边三角形,∴∠AOB=60°,AB=OB=OA,由旋转的性质得:∠AOE=30°,∴∠AOD=90°﹣30°=60°.
AC=OB,OD⊥EF,∴△AOB是等边三角形,∴∠AOB=60°,AB=OB=OA,由旋转的性质得:∠AOE=30°,∴∠AOD=90°﹣30°=60°.
在△AOB和△AOD中,∵OA=OA,∠AOB=∠AOD=60°,OB=OD,∴△AOB≌△AOD(SAS);
(2)解:四边形ABOD是菱形.理由如下:
∵△AOB≌△AOD,∴AB=AD,∴AB=AD=OB=OD,∴四边形ABOD是菱形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,D、E分别是AC、AB的中点,连接DE.点P从点D出发,沿DE方向匀速运动,速度为1cm/s;同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s.解答下列问题:
(1)当t为何值时,以点E、P、Q为顶点的三角形与△ADE相似?
(2)当t为何值时,△EPQ为等腰三角形?(直接写出答案即可);

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E分别在AB、AC上,BE与CD相交于点O,已知∠B=∠C,现添加下面的哪一个条件后,仍不能判定△ABE≌△ACD( )

A. AD=AEB. AB=AC
C. BE=CDD. ∠AEB=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在公路上行驶,看到里程表上是一个两位数,1小时后其里程表还是一个两位数,且刚好它的十位数字与个位数字与第一次看到的两位数的十位数字与个位数字颠倒了位置,又过了1小时后看到里程表是一个三位数,它是第一次看到的两位数中间加一个0,则汽车的速度是( )千米/小时.
A. 35B. 40C. 45D. 50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为![]() ;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
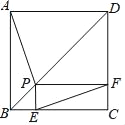
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
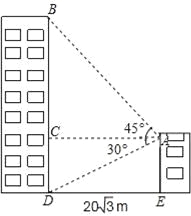
【题目】小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20![]() 米.
米.
(1)求出大厦的高度BD;
(2)求出小敏家的高度AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五名同学在一次数学测验中的平均成绩是80分,而
五名同学在一次数学测验中的平均成绩是80分,而![]() ,
,![]() ,
,![]() 三人的平均成绩是78分,下列说法一定正确的是( )
三人的平均成绩是78分,下列说法一定正确的是( )
A.![]() ,
,![]() 两人的平均成绩是83分B.
两人的平均成绩是83分B.![]() ,
,![]() 的成绩比其他三人都好
的成绩比其他三人都好
C.五人成绩的中位数一定是80分D.五人的成绩的众数一定是80分
查看答案和解析>>
科目:初中数学 来源: 题型:
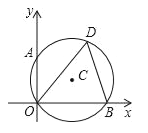
【题目】如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),D为⊙C上在第一象限内的一点且∠ODB=60°.
(1)求线段AB的长及⊙C的半径;
(2)求B点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com