
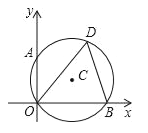
【题目】如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),D为⊙C上在第一象限内的一点且∠ODB=60°.
(1)求线段AB的长及⊙C的半径;
(2)求B点坐标.
【答案】(1)AB=4,⊙C的半径r=2;(2)(![]() ,0).
,0).
【解析】试题分析:(1)连接AB.由圆周角定理可知,AB必为⊙C的直径.Rt△ABO中,易知OA的长,而∠OAB=∠ODB=60°,通过解直角三角形,即可求得斜边AB的长,也就求得了⊙C的半径;
(2)在Rt△ABO中,由勾股定理即可求得OB的长,进而可得到B点的坐标.
试题解析:解:(1)连接AB.∵∠ODB=∠OAB,∠ODB=60°,∴∠OAB=60°.
∵∠AOB是直角,∴AB是⊙C的直径,∠OBA=30°,∴AB=2OA=4,∴⊙C的半径r=2;
(2)在Rt△OAB中,由勾股定理得:OB2+OA2=AB2,∴OB=![]() ,∴B的坐标为:(
,∴B的坐标为:(![]() ,0).
,0).


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
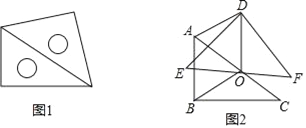
【题目】如图1,放置的一副三角尺,将含45°角的三角尺斜边中点O为旋转中心,逆时针旋转30°得到如图2,连接OB、OD、AD.
(1)求证:△AOB≌△AOD;
(2)试判定四边形ABOD是什么四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四幅图象近似刻画两个变量之间的关系,请按图象顺序将下面四种情景与之对应排序( )

①一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系)
②向锥形瓶中匀速注水(水面的高度与注水时间的关系)
③将常温下的温度计插入一杯热水中(温度计的读数与时间的关系)
④一杯越来越凉的水(水温与时间的关系)
A. ③②④①B. ③④②①C. ①④②③D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
①abc<0;②b>2a;③a+b+c=0;④8a+c>0;⑤ax2+bx+c=0的两根分别为﹣3和1.
其中正确的命题有( )
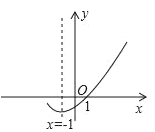
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知二次函数![]() .
.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
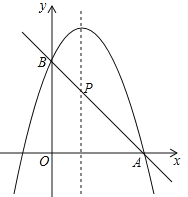
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把自然数按如图的次序排列在直角坐标系中,每个点坐标就对应着一个自然数,例如点(0,0)对应的自然数是1,点(1,2)对应的自然数是14,那么点(1,4)对应的自然数是____;点(n,n)对应的自然数是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地某月1~20日中午12时的气温(单位:℃)如下:
22 31 25 15 18 23 21 20 27 17 20 12 18 21 21 16 20 24 26 19
(1)将下列频数分布表补充完整:
气温分组 | 划记 | 频数 |
12≤x<17 |
| 3 |
17≤x<22 |
| 10 |
22≤x<27 |
| 5 |
27≤x<32 |
| 2 |

(2)补全频数分布直方图;
(3)根据频数分布表或频数分布直方图,分析数据的分布情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数y=kx的图像经过点A,点A在第四象限.过点A做AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为4.5.
(1)求该正比例函数的解析式;
(2)在x轴上是否存在一点P,使△AOP的面积为6?若存在,求点P的坐标;若不存在,请说明理由.
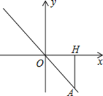
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com