
【题目】如图,在矩形ABCD中,AB=4,BC=3,点Q在BC上,BQ=2,点P是AB上的一个动点,连接PQ,将△PBQ沿PQ翻折,点B落在点B′.
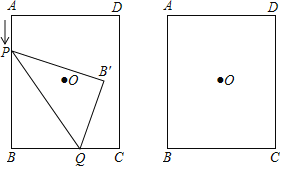
(1)当AP= 时,四边形PBQB′的面积是矩形面积的![]() ;
;
(2)当AP为何值时,四边形PBQB′是正方形?为什么?
(3)在翻折过程中是否存在AP的值,使得点B′与矩形对称中心点O重合,如果存在,请求出AP的值;如果不存在,请说明理由.
【答案】(1)3;(2)当AP为2时,四边形PBQB'是正方形;(3)存在,AP=4﹣![]() ,
,
【解析】
(1)先求得矩形ABCD的面积,可知S四边形PBQB'=6,根据折叠性质可知△PBQ的面积为3,利用三角形面积公式即可解决问题;
(2)利用正方形的性质即可解答;
(3)利用勾股定理求得BD,再利用矩形性质即可知BO,在利用勾股定理求得BE;最后利用相似即可解决问题.
解:(1)在矩形ABCD中,AB=4,BC=3,
∴S矩形ABCD=ABBC=4×3=12,
∵四边形PBQB′的面积是矩形面积的![]() ,
,
∴S四边形PBQB'=![]() S矩形ABCD=
S矩形ABCD=![]() ×12=6,
×12=6,
由折叠知,△PBQ≌△PB'Q,
∴S△PBQ=S△PB'Q=![]() S四边形PBQB'=3,
S四边形PBQB'=3,
∴BQ=3,
∴S△PBQ=![]() BQBP=
BQBP=![]() ×2BP=3,
×2BP=3,
∴BP=3,
∴AP=AB﹣BP=3,
故答案为:3;
(2)∵四边形PBQB′是正方形,
∴BP=BQ=2,
∴AP=AB﹣BP=4﹣2=2,
即:当AP为2时,四边形PBQB'是正方形;
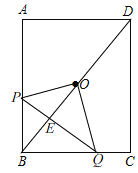
(3)存在,理由:如图,
连接BD,交PQ于E,则BD必过点O,
∵四边形ABCD是矩形,
∴ABC=∠BAD=90°,AD=BC=3,
根据勾股定理得,BD=![]() ,
,
∵O是矩形ABCD的中心,
∴BO=![]() BD=
BD=![]() ×5=
×5=![]() ,
,
当点B′与矩形对称中心点O重合时,BE=![]() BO=
BO=![]() ,
,
由折叠知,BO⊥PQ,
∴∠BEQ=90°,
在Rt△BEQ中,BQ=2,
根据勾股定理得,EQ=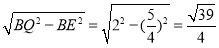 ,
,
∵∠BEQ=∠PBQ=90°,∠BQE=∠PQB,
∴△BEQ∽△PBQ,
∴![]() ,
,
∴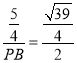 ,
,
∴PB=![]() ,
,
∴AP=AB﹣PB=4﹣![]() ,
,


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
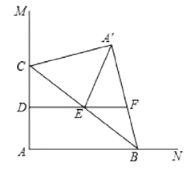
【题目】如图所示,四边形ABCD的两条对角线交于点O,且AB∥CD.有下列结论:①△AOB与△COD相似;②△ABD与△ABC相似;③S△COD∶S△AOB=DC∶AB;④S△AOD=S△BOC.其中正确的有( )
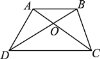
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示运算程序中,若开始输入的![]() 值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…第2017次输出的结果为( )
值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…第2017次输出的结果为( )
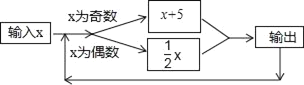
A.3B.6C.4D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
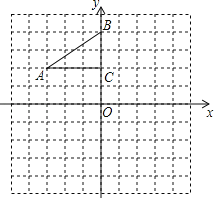
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(1,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数1至2019按照一定规律排成下表:
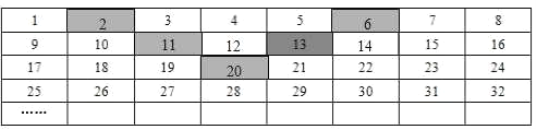
记![]() 表示第
表示第![]() 行第
行第![]() 个数,如
个数,如![]() 表示第1行第4个数是4.
表示第1行第4个数是4.
(1)直接写出![]() ,
,![]() ,
,![]() ;
;
(2)若![]() ,那么
,那么![]() ,
,![]()
(3)将表格中的5个阴影格子看成一个整体并平移,所覆盖的5个数之和能否等于2027? (填“能”或“不能”),若能,求出这5个数中的最小数,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两根木条一根长80cm另一根长60cm,把它们一端重合放在同一直线上,此时两根木条中点的距离是( )
A.10cmB.70cm或10cmC.20cmD.20cm或70cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 为边
为边![]() 上一动点,连接
上一动点,连接![]() ,
,![]() 与
与![]() 关于
关于![]() 所在直线对称,点
所在直线对称,点![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,
为直角三角形时,![]() 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
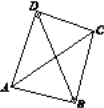
【题目】定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.
(1)如图,在损矩形ABCD中,∠ABC=∠ADC=90°,则该损矩形的直径是线段________.
(2)在损矩形ABCD内是否存在点O,使得A,B,C,D四个点都在以点O为圆心的同一个圆上?如果存在,请指出点O的具体位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
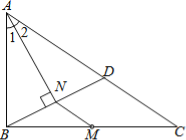
(1)求证:BN=DN;
(2)求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com