
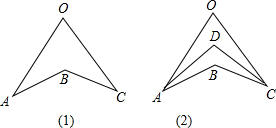
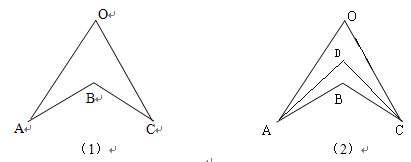
如图(1),由三角形的内角和或外角和可知:∠ABC=∠A+∠C+∠O

在图(2)中,直接利用上述的结论探究:
① AD、CD分别平分∠OAB,∠OCB,且∠O=80°∠B=120°,求∠ADC的度数 (4分)
② AD、CD分别平分∠OAB,∠OCB,猜想∠O,∠ABC,∠ADC之间的等量关系,并说明理由。(4分)
①100°②∠O+∠B=2∠D,理由见解析
解析:解:①∵∠OAB+∠OCB=∠B-∠O=120°-80°=40°
又∵AD、CD分别平分∠OAB、∠OCB
∴∠OAD+∠OCD=![]() (∠OAB+∠OCB)=
(∠OAB+∠OCB)=![]() ×40°=20° (2分)
×40°=20° (2分)
∠D=∠OAD+∠OCD+∠O=80°+20°=100° (4分)
②∠O+∠B=2∠D (1分)
理由:∵∠OAD+∠OCD=∠D-∠O
∠OAB+∠OCB=∠B-∠O
又∵AB、CD分别平分∠OAB、∠OCB
∴∠OAB+∠OCB=2(∠OAD+∠OCD)
∴2(∠D-∠O)=∠B-∠O
∴2∠D-2∠O=∠B-∠O
∴∠O+∠B=2∠D (4分)
根据三角形的外角性质和三角形内角和定理求解


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012学年福建省南平三中七年级下学期期中考试数学卷(带解析) 题型:解答题
如图(1),由三角形的内角和或外角和可知:∠ABC=∠A+∠C+∠O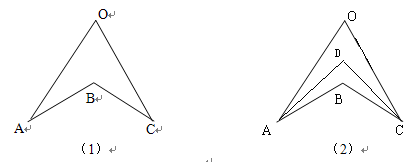
在图(2)中,直接利用上述的结论探究:
① AD、CD分别平分∠OAB,∠OCB,且∠O=80°∠B=120°,求∠ADC的度数 (4分)
② AD、CD分别平分∠OAB,∠OCB,猜想∠O,∠ABC,∠ADC之间的等量关系,并说明理由。(4分)
查看答案和解析>>
科目:初中数学 来源:2014届福建省七年级下学期期中考试数学卷(解析版) 题型:解答题
如图(1),由三角形的内角和或外角和可知:∠ABC=∠A+∠C+∠O
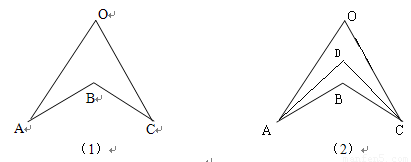
在图(2)中,直接利用上述的结论探究:
① AD、CD分别平分∠OAB,∠OCB,且∠O=80°∠B=120°,求∠ADC的度数 (4分)
② AD、CD分别平分∠OAB,∠OCB,猜想∠O,∠ABC,∠ADC之间的等量关系,并说明理由。(4分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com