
 如图,若AD、BC、EF相交于O,OA=OD,OB=OC,点E、F分别在AB、CD上,则OE=
如图,若AD、BC、EF相交于O,OA=OD,OB=OC,点E、F分别在AB、CD上,则OE=
|
|


科目:初中数学 来源: 题型:
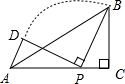 如图,在△ABC中,∠ACB=90°,AC=5,BC=3,点P是AC边上的一个动点,将线段PB绕着点P逆时针旋转90°,得到线段PD,连接AD,则线段AD的最小值等于
如图,在△ABC中,∠ACB=90°,AC=5,BC=3,点P是AC边上的一个动点,将线段PB绕着点P逆时针旋转90°,得到线段PD,连接AD,则线段AD的最小值等于查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 沙坪坝火车站将改造成一个集高铁、轻轨、公交、停车场、商业于一体的地下七层建筑,地面上欲建造一个圆形喷水池,如图,O点表示喷水池的水面中心,OA表示喷水柱子,水流从A点喷出,按如图所示的直角坐标系,每一股水流在空中的路线可以用y=-
沙坪坝火车站将改造成一个集高铁、轻轨、公交、停车场、商业于一体的地下七层建筑,地面上欲建造一个圆形喷水池,如图,O点表示喷水池的水面中心,OA表示喷水柱子,水流从A点喷出,按如图所示的直角坐标系,每一股水流在空中的路线可以用y=-| 1 |
| 2 |
| 3 |
| 2 |
| 7 |
| 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、为了解全市初中生每周“阳光体育”的时间,采取抽样调查的方式 |
| B、对“嫦娥三号”卫星零部件的检查,采取抽样调查的方式 |
| C、为了解人们保护水资源的意识,采取抽样调查的方式 |
| D、为了解全班同学的睡眠状况,采用普查的方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com