
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
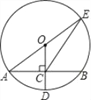
A. 2![]() B. 8 C. 2
B. 8 C. 2![]() D. 2
D. 2![]()
【答案】C
【解析】连结BE,设⊙O的半径为R,由OD⊥AB,根据垂径定理得AC=BC=![]() AB=4,在Rt△AOC中,OA=R,OC=R-CD=R-2,根据勾股定理得到(R-2)2+42=R2,解得R=5,则OC=3,由于OC为△ABE的中位线,则BE=2OC=6,再根据圆周角定理得到∠ABE=90°,然后在Rt△BCE中利用勾股定理可计算出CE.
AB=4,在Rt△AOC中,OA=R,OC=R-CD=R-2,根据勾股定理得到(R-2)2+42=R2,解得R=5,则OC=3,由于OC为△ABE的中位线,则BE=2OC=6,再根据圆周角定理得到∠ABE=90°,然后在Rt△BCE中利用勾股定理可计算出CE.
解:连结BE,设⊙O的半径为R,如图所示,
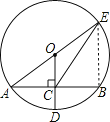
∵OD⊥AB,
∴AC=BC=![]() AB=
AB=![]() ×8=4,
×8=4,
在Rt△AOC中,OA=R,OC=R-CD=R-2,
∵OC2+AC2=OA2,
∴(R-2)2+42=R2,解得R=5,
∴OC=5-2=3,
∴BE=2OC=6,
∵AE为直径,
∴∠ABE=90°,
在Rt△BCE中, ![]() .
.
考点: 1.垂径定理;2.勾股定理;3.三角形中位线定理;4.圆周角定理.
“点睛”本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在一次汉字听写大赛中,10名学生得分情况如表:
人数 | 3 | 4 | 2 | 1 |
分数 | 80 | 85 | 90 | 9595 |
那么这10名学生所得分数的中位数和众数分别是( )
A.85和82.5
B.85.5和85
C.85和85
D.85.5和80
查看答案和解析>>
科目:初中数学 来源: 题型:
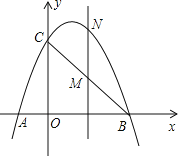
【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式。
(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N若点M的横坐标为m,请用m的代数式表示MN的长。
(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c为△ABC的三边长,且a4﹣b4+b2c2﹣a2c2=0,则△ABC的形状是( )
A. 等腰三角形 B. 直角三角形 C. 等腰直角三角形 D. 等腰三角形或直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织七年级同学到汶川地震灾区遗址参观。原计划租用25座客车若干辆,但有5人没
有座位;后来改租40座的客车,结果少用了4辆,且各辆恰好坐满.
问:该校七年级有同学多少名?原计划租用25座客车多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com