
分析 (1)先把常数项-8移项后,再左右两边同时加上一次项系数-8的一半的平方即可配方,再利用直接开平方法解方程.
(2)在左右两边同时加上一次项系数-3的一半的平方即可配方,再利用直接开平方法解方程.
解答 解:(1)x2-8x+8=0;
x2-8x=-8,
x2-8x+16=-8+16,
(x-4)2=8,
x-4=$±\sqrt{8}$,
x-4=$±2\sqrt{2}$,
x-4=2$\sqrt{2}$或x-4=-2$\sqrt{2}$,
x=4$±2\sqrt{2}$,
x1=4+2$\sqrt{2}$,x2=4-2$\sqrt{2}$;
(2)x2-3x=4,
x2-3x+$(\frac{3}{2})^{2}$=4+$(\frac{3}{2})^{2}$,
(x-$\frac{3}{2}$)2=$\frac{25}{4}$,
x-$\frac{3}{2}$=±$\frac{5}{2}$,
x-$\frac{3}{2}$=$\frac{5}{2}$或x-$\frac{3}{2}$=-$\frac{5}{2}$,
x1=4或x2=-1.
点评 此题考查了配方法的应用,掌握配方法的一般步骤是本题的关键,配方法的一般步骤是(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.


科目:初中数学 来源: 题型:解答题
 已知如图,△ABC中,AB=4,AC=2$\sqrt{2}$,∠B=30°,0°<∠C<90°.
已知如图,△ABC中,AB=4,AC=2$\sqrt{2}$,∠B=30°,0°<∠C<90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
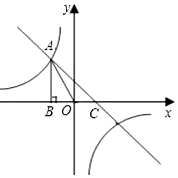 如图,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点A(-$\sqrt{3}$,2),过点A作AB⊥x轴于点B,连结AO.
如图,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点A(-$\sqrt{3}$,2),过点A作AB⊥x轴于点B,连结AO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{6}÷(\sqrt{3}-\sqrt{2})=\sqrt{2}-\sqrt{3}$ | B. | $\sqrt{(-9)×(-25)}=\sqrt{-9}×\sqrt{-25}=(-3)×(-5)=15$ | ||
| C. | $\sqrt{2}(\sqrt{3}+\sqrt{2})=\sqrt{10}$ | D. | $\sqrt{{{13}^2}-{{12}^2}}=\sqrt{(13+12)×(13-12)}=5$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com