
分析 (1)根据3000吨以内,用水每吨收费2.5元,超计划部分每吨按3元收费,即可求解;
(2)根据收费标准,分x≤3000吨,和x>3000吨两种情况进行讨论,分两种情况写出解析式;
(3)该单位缴纳水费8550元一定是超过3000元,根据超过3000吨的情况的水费标准即可得到一个关于用水量的方程,即可求解.
解答 解:(1)某月该单位用水3200吨,水费是:3000×2.5+200×3=8100元;
若用水2800吨,水费是:2800×2.5=7000元,
故答案为:8100;7000;
(2)根据题意,当0≤x≤3000时,y=2.5x;
当x>3000时,y=2.5×3000+3×(x-3000)=3x-1500,
所以y关于x的函数解析式为:$\left\{\begin{array}{l}{y=2.5x(0≤x≤3000)}\\{y=3x-1500(x>3000)}\end{array}\right.$,
(3)因为缴纳水费8550元,所以用水量应超过3000吨,故设用水x吨.
3x-1500=8550,
x=3350
即该单位这个月的用水量是3350吨.
点评 本题考查的是用一次函数解决实际问题,正确理解收费标准,列出函数解析式是关键,此类题是近年中考中的热点问题.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
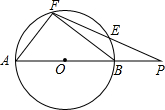 如图,点P在⊙O的直径AB的延长线上,PEF是⊙O的割线,且AF=FE,$\frac{PB}{PE}=\frac{5}{6}$,△ABF的面积为96.
如图,点P在⊙O的直径AB的延长线上,PEF是⊙O的割线,且AF=FE,$\frac{PB}{PE}=\frac{5}{6}$,△ABF的面积为96.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
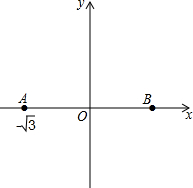 如图,在平面直角坐标系中,点A的坐标为(-$\sqrt{3}$,0),点A关于原点的对称点为B
如图,在平面直角坐标系中,点A的坐标为(-$\sqrt{3}$,0),点A关于原点的对称点为B查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com