
【题目】已知AB∥CD,点M、N分别是AB、CD上两点,点G在AB、CD之间,连接MG、NG.
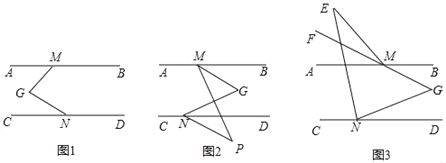
(1)如图1,若GM⊥GN,求∠AMG+∠CNG的度数;
(2)如图2,若点P是CD下方一点,MG平分∠BMP,ND平分∠GNP,已知∠BMG=30°,求∠MGN+∠MPN的度数;
(3)如图3,若点E是AB上方一点,连接EM、EN,且GM的延长线MF平分∠AME,NE平分∠CNG,2∠MEN+∠MGN=105°,求∠AME的度数.
【答案】(1)∠AMG+∠CNG=90°;(2)∠MGN+∠MPN=90°;(3)∠AME=50°.
【解析】
(1)过G作GH∥AB,依据两直线平行,内错角相等,即可得到∠AMG+∠CNG的度数;
(2)过G作GK∥AB,过点P作PQ∥AB,设∠GND=α,利用平行线的性质以及角平分线的定义,求得∠MGN=30°+α,∠MPN=60°-α,即可得到∠MGN+∠MPN=30°+α+60°-α=90°;
(3)过G作GK∥AB,过E作ET∥AB,设∠AMF=x,∠GND=y,利用平行线的性质以及角平分线的定义,可得∠MEN=∠TEN-∠TEM=90°-![]() y-2x,∠MGN=x+y,再根据2∠MEN+∠MGN=105°,即可得到2(90°-
y-2x,∠MGN=x+y,再根据2∠MEN+∠MGN=105°,即可得到2(90°-![]() y-2x)+x+y=105°,求得x=25°,即可得出∠AME=2x=50°.
y-2x)+x+y=105°,求得x=25°,即可得出∠AME=2x=50°.
(1)如图1,过G作GH∥AB,

∵AB∥CD,
∴GH∥AB∥CD,
∴∠AMG=∠HGM,∠CNG=∠HGN,
∵MG⊥NG,
∴∠MGN=∠MGH+∠NGH=∠AMG+∠CNG=90°;
(2)如图2,过G作GK∥AB,过点P作PQ∥AB,设∠GND=α,
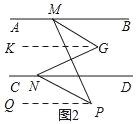
∵GK∥AB,AB∥CD,
∴GK∥CD,
∴∠KGN=∠GND=α,
∵GK∥AB,∠BMG=30°,
∴∠MGK=∠BMG=30°,
∵MG平分∠BMP,ND平分∠GNP,
∴∠GMP=∠BMG=30°,
∴∠BMP=60°,
∵PQ∥AB,
∴∠MPQ=∠BMP=60°,
∵ND平分∠GNP,
∴∠DNP=∠GND=α,
∵AB∥CD,
∴PQ∥CD,
∴∠QPN=∠DNP=α,
∴∠MGN=30°+α,∠MPN=60°﹣α,
∴∠MGN+∠MPN=30°+α+60°﹣α=90°;
(3)如图3,过G作GK∥AB,过E作ET∥AB,设∠AMF=x,∠GND=y,

∵AB,FG交于M,MF平分∠AME,
∴∠FME=∠FMA=∠BMG=x,
∴∠AME=2x,
∵GK∥AB,
∴∠MGK=∠BMG=x,
∵ET∥AB,
∴∠TEM=∠EMA=2x,
∵CD∥AB∥KG,
∴GK∥CD,
∴∠KGN=∠GND=y,
∴∠MGN=x+y,
∵∠CND=180°,NE平分∠CNG,
∴∠CNG=180°﹣y,∠CNE=![]() ∠CNG=90°﹣
∠CNG=90°﹣![]() y,
y,
∵ET∥AB∥CD,
∴ET∥CD,
∴∠TEN=∠CNE=90°﹣![]() y,
y,
∴∠MEN=∠TEN﹣∠TEM=90°﹣![]() y﹣2x,∠MGN=x+y,
y﹣2x,∠MGN=x+y,
∵2∠MEN+∠MGN=105°,
∴2(90°﹣![]() y﹣2x)+x+y=105°,
y﹣2x)+x+y=105°,
∴x=25°,
∴∠AME=2x=50°.


科目:初中数学 来源: 题型:
【题目】(本题满分10分)古运河是扬州的母亲河,为打造古运河风光带,现有一段长为180米的河道整治任务由![]() 两工程队先后接力完成.
两工程队先后接力完成.![]() 工作队每天整治12米,
工作队每天整治12米,![]() 工程队每天整治8米,共用时20天.
工程队每天整治8米,共用时20天.
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
![]()
![]()
![]()
![]() 甲:
甲: ![]() 乙:
乙:
根据甲、乙两名同学所列的方程组,请你分别指出未知数![]() 表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:![]() 表示________________,
表示________________,![]() 表示_______________;
表示_______________;
乙:![]() 表示________________,
表示________________,![]() 表示_______________.
表示_______________.
(2)求![]() 两工程队分别整治河道多少米.(写出完整的解答过程)
两工程队分别整治河道多少米.(写出完整的解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知∠ABC=30°,点D在BC上,点E在AC上,∠BAD=∠EBC, AD交BE于F.
(1)求∠BFD的度数;
(2)若EG∥AD交BC于G,EH⊥BE交BC于H,求∠HEG的度数.
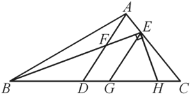
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出![]() 各点的坐标;
各点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到![]() ,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
(3)求出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴交于点A,与y轴交于点B,与直线y2=x交于点E,点E的横坐标为3.
与x轴交于点A,与y轴交于点B,与直线y2=x交于点E,点E的横坐标为3.
(1)直接写出b的值:b=______;
(2)当x取何值时,0<y1≤y2?
(3)在x轴上有一点P(m,0),过点P作x轴的垂线,与直线![]() 交于点C,与直线y2=x交于点D,若CD=2OB,求m的值.
交于点C,与直线y2=x交于点D,若CD=2OB,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).
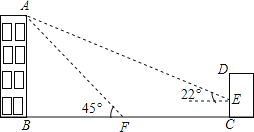
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知平行四边形ABCD顶点A的坐标为(2,6),点B在y轴上,且AD∥BC∥x轴,过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),点F(m,6)是线段AD上一动点,直线OF交BC于点E.

(1)求抛物线的表达式;
(2)设四边形ABEF的面积为S,请求出S与m的函数关系式,并写出自变量m的取值范围;
(3)如图2,过点F作FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,垂足为N,连接MN,直线AC分别交x轴,y轴于点H,G,试求线段MN的最小值,并直接写出此时m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com