
����Ŀ��������СԪ��Ƶġ���Բ��һ����Բ�����ߡ��ij߹���ͼ������
��֪����ͼ����O����O��һ��P.
����������P����O�����ߣ�


��������ͼ��
��������OP��
����ֱ��OP����ȡһ��A���Ե�AΪԲ�ģ�APΪ�뾶����A��������OP������һ��B��
�����Ӳ��ӳ�BA����A���ڵ�C��
����ֱ��PC��
��ֱ��PC��Ϊ����
����СԪ��Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2����������֤����
֤������ BC����A��ֱ����
���BPC=90�㣨____________���������������ݣ���
��OP��PC��
����OP����O�İ뾶��
��PC����O�����ߣ�____________���������������ݣ���
���𰸡���1����ȫ��ͼ�μ���������2��ֱ�����Ե�Բ�ܽ���ֱ�ǣ������뾶����˲��Ҵ�ֱ�������뾶��ֱ����Բ�����ߣ�
��������
��1��������������ͼ�μ��ɣ�
��2������Բ�ܽǶ����õ���BPC=90�㣬�������ߵ��ж��������ɵõ����ۣ�
��1����ȫͼ����ͼ��ʾ����ֱ��PC��Ϊ����
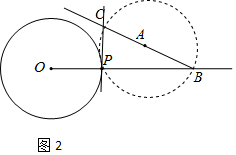
��2��֤������BC����A��ֱ����
���BPC=90�㣨Բ�ܽǶ�������
��OP��PC��
����OP����O�İ뾶��
��PC����O�����ߣ����ߵ��ж�����
�ʴ�Ϊ��Բ�ܽǶ��������ߵ��ж���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��������һ���ߵ�ƽ�������������ߵij˻������ǰ���������ν������������Σ�
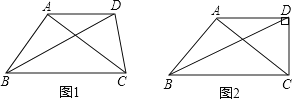
��1����֪��ABC�DZ��������Σ�AB��3��BC��4����ֱ��д����������������AC�ij���
��2����ͼ1�����ı���ABCD�У�AD��BC���Խ���BDƽ�֡�ABC����BAC����ADC����֤����ABC�DZ��������Σ�
��3����ͼ2���ڣ�2���������£�����ADC��90��ʱ�����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����̵��Գɱ�Ϊÿ��60Ԫ����һ��������ߣ���ÿ��100Ԫ�ļ۸�������ÿ�������20����Ϊ���������ۣ�����ӯ����������ٿ�棬�̵������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣���ÿ�����ÿ����5Ԫ����ÿ��ɶ���10��.
(1)���̵�ƽ��ÿ��ӯ��1200Ԫ��ÿ����ߵ��ۼ�Ӧ��Ϊ����Ԫ��
(2)���̵�Ϊ����Ч�����ÿ����ߵ��ۼ۶�Ϊ����Ԫʱ���̵�ƽ��ÿ��ӯ����ࣿ���ӯ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC��2![]() ��tanB��3����DΪ��AB��һ���㣬��ֱ��DC�Ϸ�����EDC����ECD����B���õ���EDC����CE��СֵΪ_____��
��tanB��3����DΪ��AB��һ���㣬��ֱ��DC�Ϸ�����EDC����ECD����B���õ���EDC����CE��СֵΪ_____��
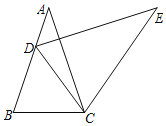
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������BC��OB����D��![]() ��һ���㣬��E��CD�е㣬����BD�ֱ�OC��OE�ڵ�F��G��
��һ���㣬��E��CD�е㣬����BD�ֱ�OC��OE�ڵ�F��G��
(1)���DGE�Ķ�����
(2)��![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��
(3)�ǡ�CFB����DGO������ֱ�ΪS1��S2����![]() ��k����
��k����![]() ��ֵ��(�ú�k��ʽ�ӱ�ʾ)
��ֵ��(�ú�k��ʽ�ӱ�ʾ)
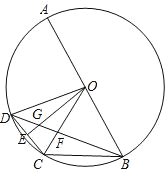
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
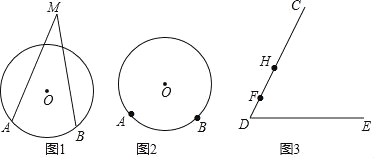
����Ŀ����ѧ����ѧϰ��Բ�ܽǵĸ�������ʣ���������Բ�ϣ�������Բ�ཻ������ͬ�����Ե�Բ�ܽ��������С���ڿκ������Բ��Ǻ�Բ�ڽǽ�����̽����
����������̽�����̣��벹��������
������������Բ�⣬������Բ�ཻ�Ľǽ���Բ��ǣ�������Բ�ڣ�������Բ�ཻ�Ľǽ���Բ�ڽǣ���ͼ1����MΪ![]() ���Ե�һ��Բ��ǣ�
���Ե�һ��Բ��ǣ�
(1)����ͼ2�л���![]() ���Ե�һ��Բ�ڽǣ�
���Ե�һ��Բ�ڽǣ�
�������
(2)ͨ����λ�ͼ��������������������룺һ�������Ե�Բ���______���������Ե�Բ�ܽǣ�һ�������Ե�Բ�ڽ�______���������Ե�Բ�ܽǣ�(������������������������С����)
����֤����
(3)����ͼ1��ͼ2��������������������ѡһ������֤����
������
����֤���������������붼����ȷ�ģ�����̽�����֣������Խ����������⣮
(4)��ͼ3��F��H�ǡ�CDE�ı�DC�����㣬�ڱ�DE����һ��Pʹ�á�FPH�����������ȷ����P��λ�ã�(д��˼·���ɣ���Ҫ��д�������ͻ�ͼ)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���Ȼ�������ֵ��![]() ���У�a�Ƿ���x2+3x+1��0�ĸ���
���У�a�Ƿ���x2+3x+1��0�ĸ���
��2����֪������y��ax2+bx+c�ĶԳ���Ϊx��2���Ҿ����㣨1��4���ͣ�5��0��������������ߵı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���P��CD���е㣬��BCD=60��������AP��BC���ӳ����ڵ�E������BP��DE�ڵ�K����O���߶�BK���е㣮
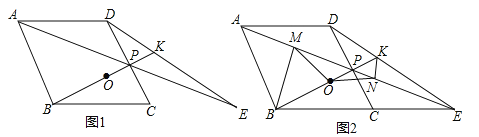
��1����֤����ADP�ա�ECP��
��2����BP=nPK�������n��ֵ��
��3����BM�AAE�ڵ�M����KN�AAE�ڵ�N������MO��NO����ͼ2��ʾ����֤����MON�ǵ��������Σ���ֱ��д����MON�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
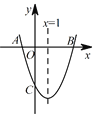
����Ŀ����ͼ����֪������y=ax2+bx��3�ĶԳ���Ϊֱ��x=1����x����A��B���㣬��y����C�㣬����B�������Ϊ(3��0)��
(1)ֱ��д��A������ꣻ
(2)����κ���y=ax2+bx��3�Ľ���ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com