
如图,抛物线C1:y=(x+m)2(m为常数,m>0),平移抛物线y=﹣x2,使其顶点D在抛物线C1位于y轴右侧的图象上,得到抛物线C2.抛物线C2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,设点D的横坐标为a.

(1)如图1,若m= .
.
①当OC=2时,求抛物线C2的解析式;
②是否存在a,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP=BP?若存在,求出a的值;若不存在,请说明理由;
(2)如图2,当OB=2 ﹣m(0<m<
﹣m(0<m< )时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).
)时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).
(1) ①y=﹣x2+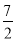 x+2.②
x+2.②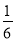 .(2)P1(
.(2)P1( ﹣m,1),P2(
﹣m,1),P2( ﹣m,﹣3),P3(﹣
﹣m,﹣3),P3(﹣ ﹣m,3),P4(3
﹣m,3),P4(3 ﹣m,3).
﹣m,3).
【解析】
试题分析:(1)①首先写出平移后抛物线C2的解析式(含有未知数a),然后利用点C(0,2)在C2上,求出抛物线C2的解析式;
②认真审题,题中条件“AP=BP”意味着点P在对称轴上,“点B与点C到直线OP的距离之和最大”意味着OP⊥BC.画出图形,如图1所示,利用三角函数(或相似),求出a的值;
(2)解题要点有3个:
i)判定△ABD为等边三角形;
ii)理论依据是角平分线的性质,即角平分线上的点到角两边的距离相等;
iii)满足条件的点有4个,即△ABD形内1个(内心),形外3个.不要漏解.
试题解析:(1)当m=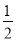 时,抛物线C1:y=(x+
时,抛物线C1:y=(x+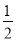 )2.
)2.
∵抛物线C2的顶点D在抛物线C1上,且横坐标为a,
∴D(a,(a+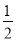 )2).
)2).
∴抛物线C2:y=﹣(x﹣a)2+(a+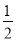 )2 (I).
)2 (I).
①∵OC=2,∴C(0,2).
∵点C在抛物线C2上,
∴﹣(0﹣a)2+(a+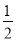 )2=2,
)2=2,
解得:a=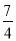 ,代入(I)式,
,代入(I)式,
得抛物线C2的解析式为:y=﹣x2+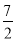 x+2.
x+2.
②在(I)式中,
令y=0,即:﹣(x﹣a)2+(a+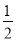 )2=0,解得x=2a+
)2=0,解得x=2a+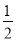 或x=﹣
或x=﹣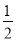 ,∴B(2a+,0);
,∴B(2a+,0);
令x=0,得:y=a+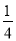 ,∴C(0,a+
,∴C(0,a+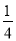 ).
).
设直线BC的解析式为y=kx+b,则有:
 ,解得
,解得 ,
,
∴直线BC的解析式为:y=﹣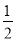 x+(a+
x+(a+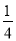 ).
).
假设存在满足条件的a值.
∵AP=BP,
∴点P在AB的垂直平分线上,即点P在C2的对称轴上;
∵点B与点C到直线OP的距离之和≤BC,只有OP⊥BC时等号成立,
∴OP⊥BC.
如图1所示,设C2对称轴x=a(a>0)与BC交于点P,与x轴交于点E,
则OP⊥BC,OE=a.
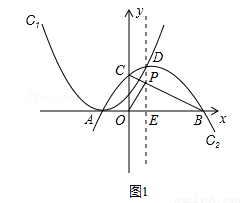
∵点P在直线BC上,
∴P(a,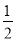 a+
a+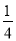 ),PE=
),PE=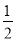 a+
a+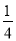 .
.
∵tan∠EOP=tan∠BCO= ,
,
∴ ,
,
解得:a=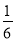 .
.
∴存在a=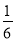 ,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP=BP
,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP=BP
(3)∵抛物线C2的顶点D在抛物线C1上,且横坐标为a,
∴D(a,(a+m)2).
∴抛物线C2:y=﹣(x﹣a)2+(a+m)2.
令y=0,即﹣(x﹣a)2+(a+m)2=0,解得:x1=2a+m,x2=﹣m,∴B(2a+m,0).
∵OB=2 ﹣m,
﹣m,
∴2a+m=2 ﹣m,
﹣m,
∴a= ﹣m.
﹣m.
∴D( ﹣m,3).
﹣m,3).
AB=OB+OA=2 ﹣m+m=2
﹣m+m=2 .
.
如图2所示,设对称轴与x轴交于点E,则DE=3,BE=AB= ,OE=OB﹣BE=
,OE=OB﹣BE= ﹣m.
﹣m.
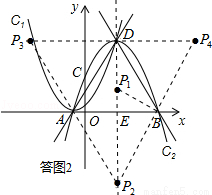
∵tan∠ABD=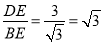 ,
,
∴∠ABD=60°.
又∵AD=BD,∴△ABD为等边三角形.
作∠ABD的平分线,交DE于点P1,则P1E=BE•tan30°= ×
×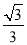 =1,
=1,
∴P1( ﹣m,1);
﹣m,1);
在△ABD形外,依次作各个外角的平分线,它们相交于点P2、P3、P4.
在Rt△BEP2中,P2E=BE•tan60°= •
• =3,
=3,
∴P2( ﹣m,﹣3);
﹣m,﹣3);
易知△ADP3、△BDP4均为等边三角形,∴DP3=DP4=AB=2 ,且P3P4∥x轴.
,且P3P4∥x轴.
∴P3(﹣ ﹣m,3)、P4(3
﹣m,3)、P4(3 ﹣m,3).
﹣m,3).
综上所述,到△ABD的三边所在直线的距离相等的所有点有4个,
其坐标为:P1( ﹣m,1),P2(
﹣m,1),P2( ﹣m,﹣3),P3(﹣
﹣m,﹣3),P3(﹣ ﹣m,3),P4(3
﹣m,3),P4(3 ﹣m,3).
﹣m,3).
【考点】二次函数综合题.


科目:初中数学 来源:2014年初中毕业升学考试(贵州黔西卷)数学(解析版) 题型:填空题
如图,将矩形纸片ABCD折叠,使边AB、CD均落在对角线BD上,得折痕BE、BF,则∠EBF= .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州贵阳卷)数学(解析版) 题型:选择题
贵阳市中小学幼儿园“爱心助残工程”第九届助残活动于2014年5月在贵阳市盲聋哑学校举行,活动当天,贵阳市盲聋哑学校获得捐赠的善款约为150000元.150000这个数用科学记数法表示为( )
A.1.5×104 B.1.5×105 C.1.5×106 D.15×104
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州六盘水卷)数学(解析版) 题型:填空题
PM2.5是指大气中的直径小于或等于0.0000025米(2.5微米)的有毒有害物质.0.0000025米用科学记数法表示为: 米.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州六盘水卷)数学(解析版) 题型:选择题
下列运算正确的是( )
A.(﹣2mn)2=4m2n2 B.y2+y2=2y4
C.(a﹣b)2=a2﹣b2 D.m2+m=m3
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(福建莆田卷)数学(解析版) 题型:解答题
如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
(1)求证:BE=CE;
(2)以点E为圆心,ED长为半径画弧,分别交BE,CE于点F,G.若BC=4,∠EBD=30°,求图中阴影部分(扇形)的面积.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(福建莆田卷)数学(解析版) 题型:填空题
在一次数学测试中,小明所在小组6人的成绩(单位:分)分别为84、79、83、87、77、81,则这6人本次数学测试成绩的中位数是
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(福建南平卷)数学(解析版) 题型:解答题
在2014年巴西世界杯足球赛开幕之前,某校团支部为了解本校学生对世界杯足球赛的关注情况,随机调查了部分学生对足球运动的喜欢程度,绘制成如下的两幅不完整的统计图.

请你根据以上统计图提供的信息,回答下列问题:
(1)随机抽查了 名学生;
(2)补全图中的条形图;
(3)若全校共有500名学生,请你估计全校大约有多少名学生喜欢(含“较喜欢”和“很喜欢”)足球运动.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(福建三明卷)数学(解析版) 题型:选择题
如图是由5个小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,这个几何体的主视图是( )


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com