
【题目】在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )
A.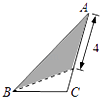
B.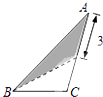
C.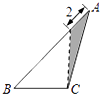
D.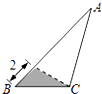
【答案】D
【解析】解:三角形纸片ABC中,AB=8,BC=4,AC=6. A、 ![]() =
= ![]() =
= ![]() ,对应边
,对应边 ![]() =
= ![]() =
= ![]() ≠
≠ ![]() ,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
B、 ![]() =
= ![]() ,对应边
,对应边 ![]() =
= ![]() =
= ![]() ≠
≠ ![]() ,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
C、 ![]() =
= ![]() =
= ![]() ,对应边
,对应边 ![]() =
= ![]() =
= ![]() ≠
≠ ![]() ,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
D、 ![]() =
= ![]() =
= ![]() ,对应边
,对应边 ![]() =
= ![]() =
= ![]() =
= ![]() ,则沿虚线剪下的涂色部分的三角形与△ABC相似,故此选项正确;
,则沿虚线剪下的涂色部分的三角形与△ABC相似,故此选项正确;
故选:D.
【考点精析】利用相似三角形的判定对题目进行判断即可得到答案,需要熟知相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.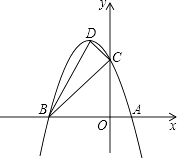
(1)求该抛物线的解析式与顶点D的坐标.
(2)试判断△BCD的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以P,A,C为顶点的三角形与△BCD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,E为BC边上一点,G为BC延长线上一点,过点E作∠AEM=60°,交∠ACG的平分线于点M.
(1)如图(1),当点E在BC边的中点位置时,通过测量AE,EM的长度,猜想AE与EM满足的数量关系是;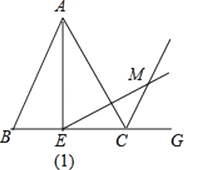
(2)如图(2),小晏通过观察、实验,提出猜想:当点E在BC边的任意位置时,始终有AE=EM.小晏把这个猜想与同学进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:在BA上取一点H使AH=CE,连接EH,要证AE=EM,只需证△AHE≌△ECM.
想法2:找点A关于直线BC的对称点F,连接AF,CF,EF.(易证∠BCF+∠BCA+ACM=180°,所以M,C,F三点在同一直线上)要证AE=EM,只需证△MEF为等腰三角形.
想法3:将线段BE绕点B顺时针旋转60°,得到线段BF,连接CF,EF,要证AE=EM,只需证四边形MCFE为平行四边形.
请你参考上面的想法,帮助小晏证明AE=EM.(一种方法即可)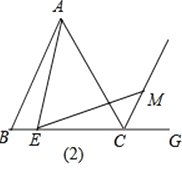
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1 , △2 , △3(图中阴影部分)的面积分别是4,9和16,则△ABC的面积是( ) 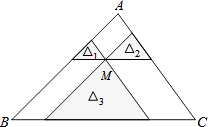
A.49
B.64
C.100
D.81
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的南偏东60°方向,距离灯塔40海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.问B处距离灯塔P有多远?(结果精确到0.1海里) (参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.449)
≈2.449)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△OAB的顶点坐标分别为(0,0),A(2,1),B(1,﹣2). 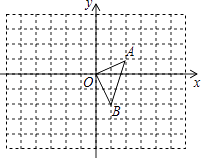
(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1 , 使它与△OAB的位似比为2:1,并分别写出点A,B的对应点A1、B1的坐标;
(2)画出将△OAB向左平移2个单位,再向上平移1个单位后得△O2A2B2 , 并写出点A,B的对应点A2、B2的坐标;
(3)判断△OA1B1和△O2A2B2是位似图形吗?若是,请在图中标出位似中心 M,并写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.“射击运动员射击一次,命中靶心”是必然事件
B.不可能事件发生的概率为0
C.随机事件发生的概率为 ![]()
D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶.已知看台高为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且∠DAB=66.5°. 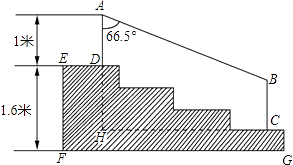
(1)求点D与点C的高度差DH;
(2)求所用不锈钢材料的总长度l.(即AD+AB+BC,结果精确到0.1米) (参考数据:sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,过点D作DE∥BC交AC的延长线于点E. 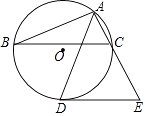
(1)试判断DE与⊙O的位置关系,并证明你的结论;
(2)若∠E=60°,⊙O的半径为5,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com