
分析 根据负整数指数幂与正整数指数幂互为倒数,非零的零次幂等于1,负数的偶数次幂是正数,相反数的意义,可化简各数,根据正数大于零,零大于负数,可得答案.
解答 解:($\frac{1}{6}$)-1=6,(-2)0=1,(-3)2=9,-|-10|=-10,
正数大于零,零大于负数,得
(-3)2>($\frac{1}{6}$)-1>(-2)0>-|-10|,
故答案为:(-3)2>($\frac{1}{6}$)-1>(-2)0>-|-10|.
点评 本题考查了负整数指数幂,利用负整数指数幂与正整数指数幂互为倒数,非零的零次幂等于1,负数的偶数次幂是正数,相反数的意义化简各数是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
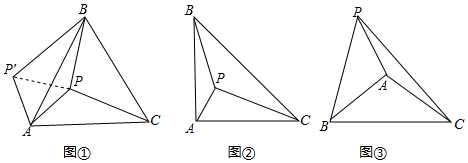
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
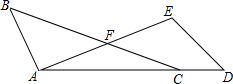 如图,点A,C,D在同一条直线上,BC与AE交于点F,FA=FC,∠D=
如图,点A,C,D在同一条直线上,BC与AE交于点F,FA=FC,∠D=查看答案和解析>>
科目:初中数学 来源: 题型:解答题
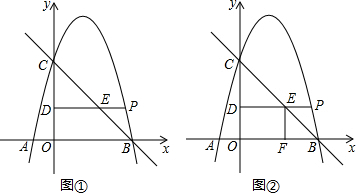
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
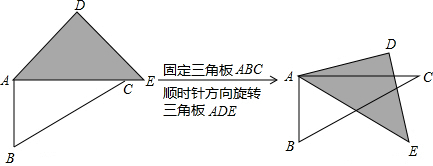
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com