
����Ŀ����֪OΪ����ԭ�㣬������y1=ax2+bx+c��a��0����x���ཻ�ڵ�A��x1��0����B��x2��0������y�ύ�ڵ�C����O��C�����ľ���Ϊ3��x1x2��0��|x1|+|x2|=4����A��C��ֱ��y2=��3x+t�ϣ�
��1����y1����x�����������ʱ�����Ա���x��ȡֵ��Χ��
��2����������y1����ƽ��n��n��0������λ����ƽ�ƺ�y����x�����������IJ���ΪP��ֱ��y2����ƽ��n����λ����ƽ�ƺ��ֱ����P�й�����ʱ����2n2��5n����Сֵ��
���𰸡���1����c=3����y��x���������ʱ��x�ܩ�1����c=��3����y��x���������ʱ��x��1����2����n=![]() ʱ��2n2��5n����СֵΪ��
ʱ��2n2��5n����СֵΪ��![]() ��
��
��������
��1���ֱ����â���C��0��3������c=3���Լ�����C��0��-3������c=-3���ó�A��B�����꣬���������������ʽ�������ó��𰸣�
��2�����â���c=3����y1=-x2-2x+3=-��x+1��2+4��y2=-3x+3���ó�y1����ƽ��n����λ�������ʽΪ��y3=-��x+1+n��2+4���������ƽ�ƺ��ֱ����P�й�����ʱ�ó�n��ȡֵ��Χ������c=-3����y1=x2-2x-3=��x-1��2-4��y2=-3x-3��y1����ƽ��n����λ�������ʽΪ��y3=��x-1+n��2-4���������ƽ�ƺ��ֱ����P�й�����ʱ�ó�n��ȡֵ��Χ�����������䷽�����������ֵ��
��1����x1x2��0��
��x1��x2��ţ�
����C��0��3������c=3��
��C��0��3������y2=��3x+t����0+t=3����t=3��
��y2=��3x+3��
��A��x1��0������y2=��3x+3����3x1+3=0��
��x1=1��
��A��1��0����
��x1��x2��ţ�x1=1��0����x2��0��
��|x1|+|x2|=4��
��1��x2=4��
��ã�x2=��3����B����3��0����
����y1=ax2+bx+3�ã�![]() ��
��
��ã�![]() ��
��
��y1=��x2��2x+3=����x+1��2+4��
��x�ܩ�1ʱ��y��x���������
����C��0����3������c=��3��
��C��0����3������y2=��3x+t����0+t=��3����t=��3��
��y2=��3x��3��
��A��x1��0��������y2=��3x��3��
��3x1��3=0��
��x1=��1��
��A����1��0����
��x1��x2��ţ�x1=��1��0����x2��0
��|x1|+|x2|=4��
��1+x2=4��
��ã�x2=3����B��3��0����
����y1=ax2+bx+3�ã�![]() ��
��
��ã�![]() ��
��
��y1=x2��2x��3=��x��1��2��4��
��x��1ʱ��y��x���������
������������c=3����y��x���������ʱ��x�ܩ�1��
��c=��3����y��x���������ʱ��x��1��
��2������c=3����y1=��x2��2x+3=����x+1��2+4��y2=��3x+3��
y1����ƽ��n����λ�������ʽΪ��y3=����x+1+n��2+4��
��x�ܩ�1��nʱ��y��x���������
y2����ƽ��n����λ�������ʽΪ��y4=��3x+3��n��
Ҫʹƽ�ƺ�ֱ����P�й����㣬��x=��1��n��y3��y4��
��������1��n+1+n��2+4�ݩ�3����1��n��+3��n��
��ã�n�ܩ�1��
��n��0����n�ܩ�1������������Ӧ��ȥ��
����c=��3����y1=x2��2x��3=��x��1��2��4��y2=��3x��3��
y1����ƽ��n����λ�������ʽΪ��y3=��x��1+n��2��4��
��x��1��nʱ��y��x���������
y2����ƽ��n����λ�������ʽΪ��y4=��3x��3��n��
Ҫʹƽ�ƺ�ֱ����P�й����㣬��x=1��n��y3��y4��
����1��n��1+n��2��4�ܩ�3��1��n����3��n��
��ã�n��1��
����������n��1��
2n2��5n=2��n��![]() ��2��
��2��![]() ��
��
�൱n=![]() ʱ��2n2��5n����СֵΪ����
ʱ��2n2��5n����СֵΪ����![]() ��
��


 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ���������½��ۣ���b2��4ac����abc��0����2a��b=0����8a+c��0����9a+3b+c��0�����н�����ȷ������ ����������ȷ���۵���ţ�
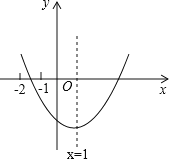
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������ABC�У���D��E�ֱ��ڱ�AC��AB�ϣ�AG��BC�ڵ�G��AF��DE�ڵ�F����EAF=��GAC��
��1����֤����ADE�ס�ABC��
��2����AD=3��AB=5����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+��2��a��x��2��a��0����ͼ����x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����y�ύ�ڵ�C���������н��ۣ�
����a��0�������£�����aȡ��ֵ����A��һ�����㣻
����a��0�������£�����aȡ��ֵ�������ߵĶԳ���һ��λ��y�����ࣻ
��y����Сֵ�����ک�2��
����AB=AC����a=![]() ��
��
������ȷ�Ľ����У�����������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
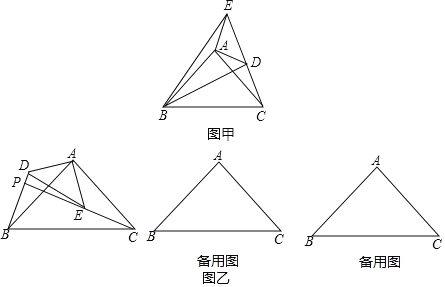
����Ŀ����ͼ�ң���ABC �͡�ADE ���й�������ĵ���ֱ�������Σ���BAC=��DAE=90�㣬��PΪ���� BD��CE�Ľ��㣮
��1����ͼ�ף�����ADE �Ƶ�A ��ת���� C��D��E ��ͬһ��ֱ����ʱ������BD��BE�������и������ĸ������У�������ȷ�����ļ��������ش�ֱ��д��ţ�
��BD=CE����BD��CE���ۡ�ACE+��DBC=45�㣻��BE2=2(AD2+AB2)
��2���� AB=4��AD=2���ѡ�ADE �Ƶ� A ��ת��
�ٵ���CAE=90��ʱ���� PB �ij���
��ֱ��д����ת�������߶� PB �������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
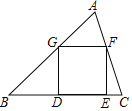
����Ŀ����ͼ����֪������DEFG�Ķ���D��E��![]() �ı�BC�ϣ�����G��F�ֱ��ڱ�AB��AC��
�ı�BC�ϣ�����G��F�ֱ��ڱ�AB��AC��![]() ���
���![]() ��
��![]() �������6����ô��������εı߳���
�������6����ô��������εı߳���![]() ����
����![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�н�����һ�鳤Ϊ60�ף���Ϊ50�ľ��λĵأ��ط��������ڴ˽�һ���ۺ������й㳡��������Ӱ����Ϊͨ����ͨ���Ŀ��Ⱦ���ȣ��м���������Σ������������ε�һ�߳���Ϊa�ף����������ܽ�������Ϊ�˶����أ���ͨ���Ŀ���Ϊx�ף�

��1��a�� ���ú�x�Ĵ���ʽ��ʾ����
��2�����ܽ��˶�������ռ�����Ϊ 2430ƽ���ף���ͨ���Ŀ���Ϊ�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�У���A=30������ͬһƽ���ڣ��ԶԽ���BDΪ�ױ�������Ϊ120���ĵ���������BDE������EBC�Ķ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
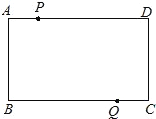
����Ŀ����ͼ��ʾ���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�![]() ��
��![]() ������P��Q�ֱ�ͬʱ��A��C��������P��3cm/s���ٶ���D�ƶ���ֱ��DΪֹ��Q��2cm/s���ٶ���B�ƶ�.
������P��Q�ֱ�ͬʱ��A��C��������P��3cm/s���ٶ���D�ƶ���ֱ��DΪֹ��Q��2cm/s���ٶ���B�ƶ�.
��1��P��Q����ӳ�����ʼ������ı���ABQP������Ǿ��������![]() ��
��
��2��P��Q�ӿ�ʼ���������![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com