
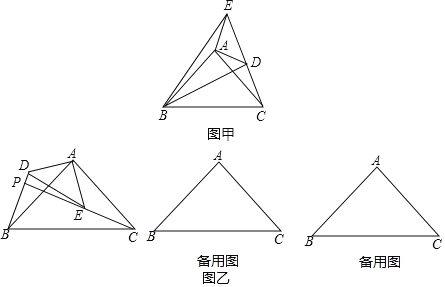
【题目】如图乙,△ABC 和△ADE 是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线 BD,CE的交点.
(1)如图甲,将△ADE 绕点A 旋转,当 C、D、E 在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是哪几个.(回答直接写序号)
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2)
(2)若 AB=4,AD=2,把△ADE 绕点 A 旋转,
①当∠CAE=90°时,求 PB 的长;
②直接写出旋转过程中线段 PB 长的最大值.
【答案】(1)①②③;(2)①PB=![]() 或
或![]() ,②PB长的最小值是
,②PB长的最小值是![]() -2,最大值是
-2,最大值是![]() +2.
+2.
【解析】
(1)①由条件证明△ABD≌△ACE,就可以得到结论②由△ABD≌△ACE就可以得出∠ABD=∠ACE,就可以得出∠BDC=90°,进而得出结论;③由条件知∠ABC=∠ABD+∠DBC=45°,由∠ABD=∠ACE就可以得出结论;④△BDE为直角三角形就可以得出BE2=BD2+DE2,由△DAE和△BAC是等腰直角三角形就有DE2=2AD2,BC2=2AB2,就有BC2=BD2+CD2≠BD2就可以得出结论;
(2)①分两种情形a、如图乙-1中,当点E在AB上时,BE=AB-AE=2.由△PEB∽△AEC,得![]() =
=![]() ,由此即可解决问题.b、如图乙-2中,当点E在BA延长线上时,BE=6.解法类似;
,由此即可解决问题.b、如图乙-2中,当点E在BA延长线上时,BE=6.解法类似;
②如图乙-3中,以A为圆心AD为半径画圆,当CE在⊙A上方与⊙A相切时,PB的值最大.分别求出PB即可.
(1)①②③;
(2)①解:a、如图2中,当点E在AB上时,BE=AB-AE=2.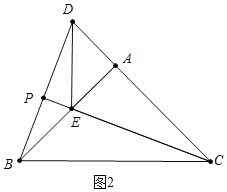
∵∠EAC=90°,
∴CE=![]() ,
,
同(1)可证△ADB≌△AEC.
∴∠DBA=∠ECA.
∵∠PEB=∠AEC,
∴△PEB∽△AEC.
∴![]() ,
,
∴![]() ,
,
∴PB=![]()
b、如图3中,当点E在BA延长线上时,BE=6.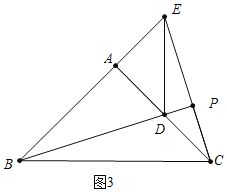
∵∠EAC=90°,
∴CE=![]() ,
,
同(1)可证△ADB≌△AEC.
∴∠DBA=∠ECA.
∵∠BEP=∠CEA,
∴△PEB∽△AEC,
∴![]() ,
,
∴![]() ,
,
∴PB=![]() ,
,
综上,PB=![]() 或
或![]() .
.
②解:a、如图4中,以A为圆心AD为半径画圆,当CE在⊙A下方与⊙A相切时,PB的值最小.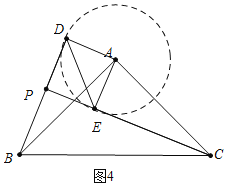
理由:此时∠BCE最小,因此PB最小,(△PBC是直角三角形,斜边BC为定值,∠BCE最小,因此PB最小)
∵AE⊥EC,
∴EC=![]() ,
,
由(1)可知,△ABD≌△ACE,
∴∠ADB=∠AEC=90°,BD=CE=2![]() ,
,
∴∠ADP=∠DAE=∠AEP=90°,
∴四边形AEPD是矩形,
∴PD=AE=2,
∴PB=BD-PD=2![]() -2.
-2.
b、如图5中,以A为圆心AD为半径画圆,当CE在⊙A上方与⊙A相切时,PB的值最大.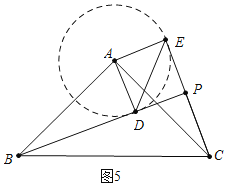
理由:此时∠BCE最大,因此PB最大,(△PBC是直角三角形,斜边BC为定值,∠BCE最大,因此PB最大)
∵AE⊥EC,
∴EC=![]() ,
,
由(1)可知,△ABD≌△ACE,
∴∠ADB=∠AEC=90°,BD=CE=![]() ,
,
∴∠ADP=∠DAE=∠AEP=90°,
∴四边形AEPD是矩形,
∴PD=AE=2,
∴PB=BD+PD=![]() +2.
+2.
综上所述,PB长的最小值是![]() -2,最大值是
-2,最大值是![]() +2.
+2.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:
①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,
其中,正确的个数有( )
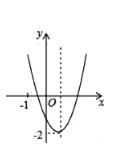
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 今年清明节前后某茶叶销售商在青山茶厂先后购进两批茶叶.第一批茶叶进货用了5.4万元,进货单价为a元/千克.购回后该销售商将茶叶分类包装出售,把其中300千克精装品以进货单件的两倍出售;余下的简装品以150元/千克的价格出售,全部卖出.第二批进货用了5万元,这一次的进货单价每千克比第一批少了20元.购回分类包装后精装品占总质量的一半,以200元/千克的单价出售;余下的简装品在这批进货单价的基础上每千克加价40元后全部卖出.若其它成本不计,第二批茶叶获得的毛利润是3.5万元.
(1)用含a的代数式表示第一批茶叶的毛利润;
(2)求第一批茶叶中精装品每千克售价.(总售价-总进价=毛利润)
查看答案和解析>>
科目:初中数学 来源: 题型:
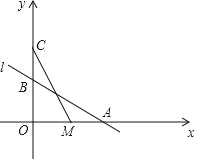
【题目】如图,直线l:y=﹣![]() x+2与x轴,y轴分別交于点A,B,在y轴上有一点C(0,4),动点M从点A出发以毎秒1个単位长度的速度沿x轴向左运动,设运动的时间为t秒.
x+2与x轴,y轴分別交于点A,B,在y轴上有一点C(0,4),动点M从点A出发以毎秒1个単位长度的速度沿x轴向左运动,设运动的时间为t秒.
(1)求点A的坐标;
(2)请从A,B两题中任选一题作答.
A.求△COM的面积S与时间t之间的函数表达式;
B.当△ABM为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分.根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:
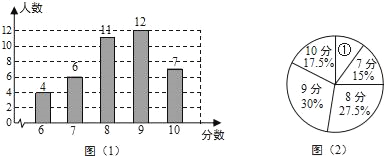
(Ⅰ)扇形 ①的圆心角的大小是 ;
(Ⅱ)求这40个样本数据的平均数、众数、中位数;
(Ⅲ)若该校九年级共有320名学生,估计该校理化实验操作得满分(10分)有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A(x1,0),B(x2,0),与y轴交于点C,且O,C两点间的距离为3,x1x2<0,|x1|+|x2|=4,点A,C在直线y2=﹣3x+t上.
(1)当y1随着x的增大而增大时,求自变量x的取值范围;
(2)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求2n2﹣5n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传节约用水,小强随机调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
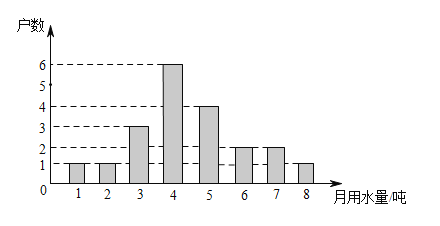
(1)小明一共调查了多少户家庭?
(2)求所调查家庭3月份用水量的众数、中位数和平均数;
(3)若该小区有800户居民,请你估计这个小区3月份的总用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 在平面直角坐标系中的位置如图所示,且三个顶点都在正方形网格的格点上.
在平面直角坐标系中的位置如图所示,且三个顶点都在正方形网格的格点上.
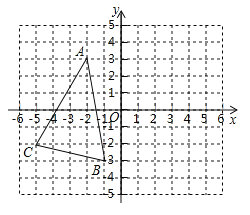
(1)把![]() 沿
沿![]() 轴翻折得到
轴翻折得到![]() ,画出
,画出![]() ,并写出点
,并写出点![]() 的坐标_____;
的坐标_____;
(2)若点![]() 在
在![]() 内部,当
内部,当![]() 沿
沿![]() 轴翻折后,点
轴翻折后,点![]() 对应点
对应点![]() 的坐标是_____;
的坐标是_____;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“八荣八耻”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.

(1)根据下图,分别求出两班复赛的平均成绩和方差;
(2)根据(1)的计算结果,分析哪个班级的复赛成绩较好?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com