
【题目】为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分.根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:
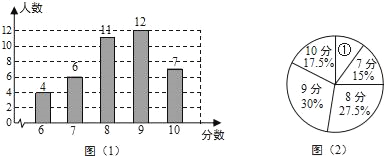
(Ⅰ)扇形 ①的圆心角的大小是 ;
(Ⅱ)求这40个样本数据的平均数、众数、中位数;
(Ⅲ)若该校九年级共有320名学生,估计该校理化实验操作得满分(10分)有多少人.
【答案】(1)36°;(2)平均数是8.3,众数是9,中位数是8;(3)得满分约有56人
【解析】
(1)用360°乘以①所占百分比即可得解;
(2)根据平均数的定义计算出平均数;找出这组数据中出现次数最多的即为众数;把数据从小到大的顺序排列,找出中位数即可;
(3)用九年级总人数乘以得满分人数所占百分比即可得解.
(Ⅰ)360°×(1﹣15%﹣27.5%﹣30%﹣17.5%)
=360°×10%
=36°;
故答案为:36°;
(Ⅱ)∵![]() =
=![]() =8.3,
=8.3,
∴平均数是8.3,
∵9出现了12次,次数最多,
∴众数是9,
∵将40个数字按从小到大排列,中间的两个数都是8,
∴中位数是![]() =8;
=8;
(Ⅲ)∵320×17.5%=56,
∴满分约有56人.


科目:初中数学 来源: 题型:
【题目】某文教用品商店欲购进![]() 、
、![]() 两种笔记本,用
两种笔记本,用![]() 元购进的
元购进的![]() 种笔记本与用
种笔记本与用![]() 元购进的
元购进的![]() 种笔记本的数量相同,每本
种笔记本的数量相同,每本![]() 种笔记本的进价比每本
种笔记本的进价比每本![]() 种笔记本的进价贵
种笔记本的进价贵![]() 元.
元.
(1)求![]() 、
、![]() 两种笔记本每本的进价分别为多少元?
两种笔记本每本的进价分别为多少元?
(2)若该商店![]() 种笔记本每本售价
种笔记本每本售价![]() 元,
元,![]() 种笔记本每本售价
种笔记本每本售价![]() 元,准备购进
元,准备购进![]() 、
、![]() 两种笔记本共
两种笔记本共![]() 本,且这两种笔记本全部售出后总获利不小于
本,且这两种笔记本全部售出后总获利不小于![]() 元,则最多购进
元,则最多购进![]() 种笔记本多少本?
种笔记本多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 小明遇到这样一个问题
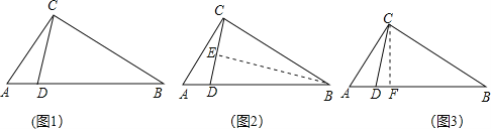
如图1,△ABC中,∠ACB=90°,点D在AB上,且BD=BC,求证:∠ABC=2∠ACD.
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法2:如图2,作BE⊥CD,垂足为点E.
方法3:如图3,作CF⊥AB,垂足为点F.
根据阅读材料,从三种方法中任选一种方法,证明∠ABC=2∠ACD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,A(0,4),B(8,0),C(8,4).
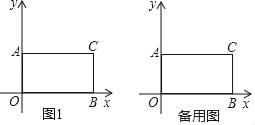
(1)试说明四边形AOBC是矩形.
(2)在x轴上取一点D,将△DCB绕点C顺时针旋转90°得到△D'CB'(点D'与点D对应).
①若OD=3,求点D'的坐标.
②连接AD'、OD',则AD'+OD'是否存在最小值,若存在,请直接写出最小值及此时点D'的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕交OA于点C,则弧AD的长为( )
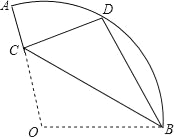
A. 2π B. 3π C. 4π D. 5π
查看答案和解析>>
科目:初中数学 来源: 题型:
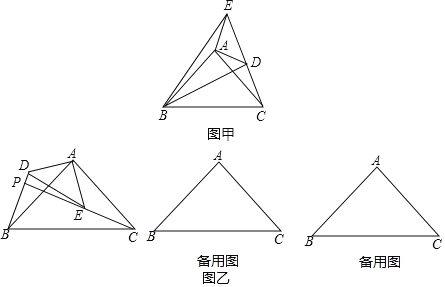
【题目】如图乙,△ABC 和△ADE 是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线 BD,CE的交点.
(1)如图甲,将△ADE 绕点A 旋转,当 C、D、E 在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是哪几个.(回答直接写序号)
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2)
(2)若 AB=4,AD=2,把△ADE 绕点 A 旋转,
①当∠CAE=90°时,求 PB 的长;
②直接写出旋转过程中线段 PB 长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次篮球比赛中,如图队员甲正在投篮.已知球出手时离地面![]() m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,对方队员乙在甲面前1 m处跳起盖帽拦截,已知乙的最大摸高为3.1 m,那么他能否获得成功?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,O为坐标原点,A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com