
【题目】如图1,在平面直角坐标系xOy中,A(0,4),B(8,0),C(8,4).
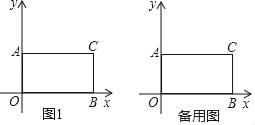
(1)试说明四边形AOBC是矩形.
(2)在x轴上取一点D,将△DCB绕点C顺时针旋转90°得到△D'CB'(点D'与点D对应).
①若OD=3,求点D'的坐标.
②连接AD'、OD',则AD'+OD'是否存在最小值,若存在,请直接写出最小值及此时点D'的坐标;若不存在,请说明理由.
【答案】(1)见解析;(2)①D'的坐标为(4,9),②AD'+OD'的最小值是![]() 或4
或4![]() ,点D'的坐标是(4,2).
,点D'的坐标是(4,2).
【解析】
(1)根据矩形的判定证明即可;
(2)①当点D在原点右侧时,根据旋转的性质和矩形的性质解答即可;②当点D在原点左侧时,根据旋转的性质和矩形的性质解答即可.
(1)∵A(0,4),B(8,0),C(8,4).
∴OA=4,BC=4,OB=8,AC=8,
∴OA=BC,AC=OB,
∴四边形AOBC是平行四边形,
∵∠AOB=90°,
∴AOBC是矩形;
(2)∵AOBC是矩形,
∴∠ACB=90°,∠OBC=90°,
∵△D'CB'将△DCB绕点C顺时针旋转90°得到(点D'与点D对应),
∴∠D'B'C=∠DBC=90°,B'C=BC=4,D'B'=DB,∠BCB'=90°,
即点B'在AC边上,
∴D'B'⊥AC,
①如图1,当点D在原点右侧时:D'B'=DB=8﹣3=5,

∴点D'的坐标为(4,9);
②如图2,当点D在原点左侧时:D'B'=DB=8+3=11,
∴点D'的坐标为(4,15),
综上所述:点D'的坐标为(4,9)或(4,15).
AD'+OD'的最小值是![]() (或4
(或4![]() ),
),
点D'的坐标是(4,2).


科目:初中数学 来源: 题型:
【题目】如图①,在Rt△ABC中,∠ABC=90o,AB是⊙O的直径,⊙O交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,∠A=∠PDB.
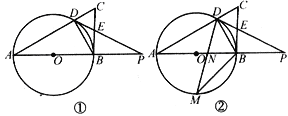
(1)求证:PD是⊙O的切线;
(2)若AB=4,DA=DP,试求弧BD的长;
(3)如图②,点M是弧AB的中点,连结DM,交AB于点N.若tanA=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
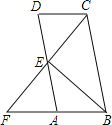
【题目】如图,四边形ABCD中,CD∥AB,E是AD中点,CE交BA延长线于点F.
(1)试说明:CD=AF;
(2)若BC=BF,试说明:BE⊥CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 今年清明节前后某茶叶销售商在青山茶厂先后购进两批茶叶.第一批茶叶进货用了5.4万元,进货单价为a元/千克.购回后该销售商将茶叶分类包装出售,把其中300千克精装品以进货单件的两倍出售;余下的简装品以150元/千克的价格出售,全部卖出.第二批进货用了5万元,这一次的进货单价每千克比第一批少了20元.购回分类包装后精装品占总质量的一半,以200元/千克的单价出售;余下的简装品在这批进货单价的基础上每千克加价40元后全部卖出.若其它成本不计,第二批茶叶获得的毛利润是3.5万元.
(1)用含a的代数式表示第一批茶叶的毛利润;
(2)求第一批茶叶中精装品每千克售价.(总售价-总进价=毛利润)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某公司的一批某品牌衬衣的质量抽检结果如下:
抽检件数 | 50 | 100 | 200 | 300 | 400 | 500 |
次品件数 | 0 | 4 | 16 | 19 | 24 | 30 |
(1)请结合表格数据直接写出这批衬衣中任抽1件是次品的概率.
(2)如果销售这批衬衣600件,至少要准备多少件正品衬衣供买到次品的顾客退换?
查看答案和解析>>
科目:初中数学 来源: 题型:
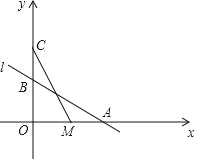
【题目】如图,直线l:y=﹣![]() x+2与x轴,y轴分別交于点A,B,在y轴上有一点C(0,4),动点M从点A出发以毎秒1个単位长度的速度沿x轴向左运动,设运动的时间为t秒.
x+2与x轴,y轴分別交于点A,B,在y轴上有一点C(0,4),动点M从点A出发以毎秒1个単位长度的速度沿x轴向左运动,设运动的时间为t秒.
(1)求点A的坐标;
(2)请从A,B两题中任选一题作答.
A.求△COM的面积S与时间t之间的函数表达式;
B.当△ABM为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分.根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:
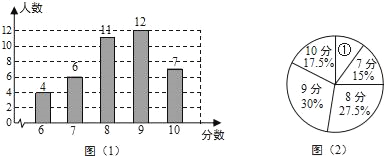
(Ⅰ)扇形 ①的圆心角的大小是 ;
(Ⅱ)求这40个样本数据的平均数、众数、中位数;
(Ⅲ)若该校九年级共有320名学生,估计该校理化实验操作得满分(10分)有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传节约用水,小强随机调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
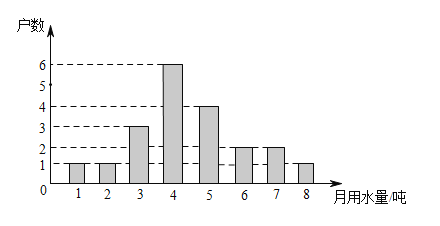
(1)小明一共调查了多少户家庭?
(2)求所调查家庭3月份用水量的众数、中位数和平均数;
(3)若该小区有800户居民,请你估计这个小区3月份的总用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 E,F,G,H 分别是任意四边形 ABCD 中 AD,BD,CA,BC 的中点. 若四边形 EFGH 是菱形,则四边形 ABCD 的边需满足的条件是( )
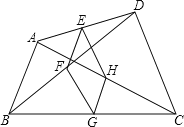
A. AB∥DC B. AC=BD C. AC⊥BD D. AB=DC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com