
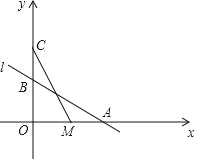
【题目】如图,直线l:y=﹣![]() x+2与x轴,y轴分別交于点A,B,在y轴上有一点C(0,4),动点M从点A出发以毎秒1个単位长度的速度沿x轴向左运动,设运动的时间为t秒.
x+2与x轴,y轴分別交于点A,B,在y轴上有一点C(0,4),动点M从点A出发以毎秒1个単位长度的速度沿x轴向左运动,设运动的时间为t秒.
(1)求点A的坐标;
(2)请从A,B两题中任选一题作答.
A.求△COM的面积S与时间t之间的函数表达式;
B.当△ABM为等腰三角形时,求t的值.
【答案】(1)A(4,0)、B(0,2)(2)A、当0≤t≤4时,8﹣2t;当t>4时,2t﹣8;B、![]() s或2
s或2![]() s或8s.
s或8s.
【解析】
(1)由直线L的函数解析式,令y=0求A点坐标,x=0求B点坐标;
(2)A、由面积公式S=![]() OMOC求出S与t之间的函数关系式;
OMOC求出S与t之间的函数关系式;
B、△ABM是等腰三角形,有三种情形,分别求解即可.
(1)对于直线AB:y=﹣![]() x+2,
x+2,
当x=0时,y=2,
当y=0时,x=4,
则A、B两点的坐标分别为A(4,0)、B(0,2);
(2)A、∵C(0,4),A(4,0),
∴OC=OA=4,
当0≤t≤4时,OM=OA﹣AM=4﹣t,S△OCM=![]() ×4×(4﹣t)=8﹣2t;
×4×(4﹣t)=8﹣2t;
当t>4时,OM=AM﹣OA=t﹣4,S△OCM=![]() ×4×(t﹣4)=2t﹣8;
×4×(t﹣4)=2t﹣8;
B、△ABM是等腰三角形,有三种情形:
①当BM=AM时,设BM=AM=x,则OM=4﹣x,
在Rt△OBM中,∵OB2+OM2=BM2,
∴22+(4﹣x)2=x2,
∴x=![]() ,
,
∴AM=![]() ,
,
∴t=![]() 时,△ABM是等腰三角形;
时,△ABM是等腰三角形;
②当AM′=AB=![]() =2
=2![]() 时,即t=2
时,即t=2![]() 时,△ABM是等腰三角形;
时,△ABM是等腰三角形;
③当BM″=BA时,∵OB⊥AM″,
∴OM″=OA=4,
∴AM″=8,
∴t=8时,△ABM是等腰三角形,
综上所述,满足条件的t的值为![]() s或2
s或2![]() s或8s.
s或8s.


科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°. 
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )
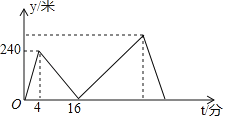
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班去体育用品商店购买羽毛球和羽毛球拍,每只羽毛球2元,每副羽毛球拍25元.甲商店说:“羽毛球拍和羽毛球都打9折优惠”,乙商店说:“买一副羽毛球拍赠2只羽毛球”.
(1)该班如果买2副羽毛球拍和20只羽毛球,问在甲、乙两家商店各需花多少钱?
(2)该班如果准备花90元钱全部用于买2副羽毛球拍和若干只羽毛球,请问到哪家商店购买更合算?
(3)该班如果必须买2副羽毛球拍,问当买多少只羽毛球时到两家商店购买同样合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D在边BC上,以A为圆心,AD长为半径画圆弧,交边BC的另一点E,交边AC于F,连接AE,EF. 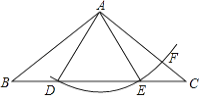
(1)求证:△ABD≌△ACE;
(2)若∠ADB=3∠CEF,请判断EF与AB有怎样的位置关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在公路上匀速行驶,下表记录的是汽车在加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x(时) | 0 | 1 | 2 | 2.5 |
余油量y(升) | 100 | 80 | 60 | 50 |
(1)小明分析上表中所给的数据发现x,y成一次函数关系,试求出它们之间的函数表达式(不要求写出自变量的取值范围);
(2)求汽车行驶4.2小时后,油箱内余油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论: ①△AED≌△DFB;②S四边形BCDG= ![]() CG2;③若AF=2DF,则BG=6GF.
CG2;③若AF=2DF,则BG=6GF.
其中正确的结论( )
A.只有①②
B.只有①③
C.只有②③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A和点F,点B和点E分别是反比例函数y= ![]() 图象在第一象限和第三象限上的点,过点A,B作AC⊥x轴,BD⊥x轴,垂足分别为点C、D,CD=6,且AF=FC,DE=BE,已知四边形ADCF的面积是四边形BCDE的面积的2倍,则OC的长为 .
图象在第一象限和第三象限上的点,过点A,B作AC⊥x轴,BD⊥x轴,垂足分别为点C、D,CD=6,且AF=FC,DE=BE,已知四边形ADCF的面积是四边形BCDE的面积的2倍,则OC的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为( ).

A. 9 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com