
【题目】已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为( ).

A. 9 B. 3 C. ![]() D.
D. ![]()
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
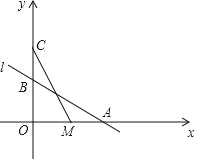
【题目】如图,直线l:y=﹣![]() x+2与x轴,y轴分別交于点A,B,在y轴上有一点C(0,4),动点M从点A出发以毎秒1个単位长度的速度沿x轴向左运动,设运动的时间为t秒.
x+2与x轴,y轴分別交于点A,B,在y轴上有一点C(0,4),动点M从点A出发以毎秒1个単位长度的速度沿x轴向左运动,设运动的时间为t秒.
(1)求点A的坐标;
(2)请从A,B两题中任选一题作答.
A.求△COM的面积S与时间t之间的函数表达式;
B.当△ABM为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC的平分线分别交AD、AC于点E,F,则 ![]() 的值是( )
的值是( ) 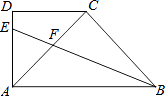
A.![]()
B.![]()
C.![]() +1
+1
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A的直线作垂线,垂足分别为E、F.
(1)求证:△ABE≌△CAF
(2)如图①过A的直线与斜边BC不相交时,试探索EF、 BE、CF三条线段的关系;
(3)如图②过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,求FE长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架云梯长25米,斜靠在一面墙上,梯子靠墙的一端距地面24米。(1)这个梯子底端离墙多少米?(2)如果梯子的顶端下滑了4米,那么梯子的底部在水平方向也滑动了4米吗?如果不是,那滑动了几米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线y=![]() x﹣3分别与x轴、y轴分别交于点A和点B,M是OB上一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线B′M的解析式为_____.
x﹣3分别与x轴、y轴分别交于点A和点B,M是OB上一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线B′M的解析式为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A、B在数轴上对应的数分别用a、b表示,且(a﹣20)2+|b+10|=0,P是数轴上的一个动点.
(1)在数轴上标出A、B的位置,并求出A、B之间的距离;
(2)已知线段OB上有点C且|BC|=6,当数轴上有点P满足PB=2PC时,求P点对应的数;
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,…….点P能移动到与A或B重合的位置吗?若不能,请直接回答;若能,请直接指出,第几次移动,与哪一点重合.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com