练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】解不等式组 并求它的整数解．

    【答案】解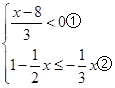： ， 由①得：x＜8，
    由②得：x≥6，
    ∴不等式组的解集为6≤x＜8，
    则不等式组的整数解为6，7
    【解析】分别求出不等式组中两不等式的解集，找出解集的公共部分确定出不等式组的解集，确定出整数解即可．
    【考点精析】掌握一元一次不等式组的解法和一元一次不等式组的整数解是解答本题的根本，需要知道解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )；使不等式组中的每个不等式都成立的未知数的值叫不等式组的解，一个不等式组的所有的解组成的集合，叫这个不等式组的解集(简称不等式组的解)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一辆汽车在公路上匀速行驶，下表记录的是汽车在加满油后油箱内余油量y（升）与行驶时间x（时）之间的关系：

    行驶时间x（时）

    0

    1

    2

    2.5

    余油量y（升）

    100

    80

    60

    50

    （1）小明分析上表中所给的数据发现x，y成一次函数关系，试求出它们之间的函数表达式（不要求写出自变量的取值范围）；

    （2）求汽车行驶4.2小时后，油箱内余油多少升？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A、B两地相距450千米，甲、乙两车分别从A、B两地同时出发，相向而行．已知甲车的速度为100千米/时，乙车的速度为80千米/时，___________小时后两车相距30千米．

    【答案】或

    【解析】

    应该有两种情况，第一次应该还没相遇时相距30千米，第二次应该是相遇后交错离开相距30千米，根据路程=速度×时间，可列方程求解．

    设第一次相距30千米时，经过了x小时，

    由题意，得（100+80）x=450-30，

    解得x=；

    设第二次相距30千米时，经过了y小时，

    由题意，得（100+80）y=450+30，

    解得y=，

    故经过小时或小时相距30千米．

    故答案为：或

    【点睛】

    本题考查理解题意能力，关键知道相距30千米时有两次以及知道路程=速度×时间，以路程做为等量关系可列方程求解．

    【题型】填空题
    【结束】
    18

    【题目】如图，一个长方体的表面展开图中四边形ABCD是正方形(正方形的四个角都是直角、四条边都相等)，则根据图中数据可得原长方体的体积是_________cm3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：(x-2)-(4x-1)=4.

    【答案】x=-.

    【解析】

    方程两边都乘以6去分母后，去括号，移项合并，将x系数化为1即可求出解.

    去分母得：3（x-2）-2（4x-1）=24，

    去括号得：3x-6-8x+2=24，

    移项合并得：-5x=28，

    解得：x=-.

    【点睛】

    此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，将x系数化为1，求出解．

    【题型】解答题
    【结束】
    22

    【题目】（1）已知a+b=5，ab=-2，求代数式（6a-3b-2ab）-（a-8b-ab）的值；

    （2）已知2x-y-4=0，求9x27y÷81y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形．若斜边AB＝3,则图中阴影部分的面积为（ ）.

    A. 9 B. 3 C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，图1是由5个完全相同的正方体搭成的几何体，现将标有E的正方体平移至图2所示的位置，下列说法中正确的是（ ）
    ①左、右两个几何体的主视图相同
    ②左、右两个几何体的俯视图相同
    ③左、右两个几何体的左视图相同．

    A.①②③
    B.②③
    C.①②
    D.①③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1）是一个六角星的纸板，其中六个锐角都为60°，六个钝角都为120°，每条边都相等，现将该纸板按图（2）切割，并无缝隙无重叠地拼成矩形ABCD．若六角星纸板的面积为9 cm2 ， 则矩形ABCD的周长为（ ）
    A.18cm
    B.8 cm
    C.（2 +6）cm
    D.（6 +6）cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算

    （1）8﹣（﹣2）

    （2）1﹣6+（﹣20）﹣（﹣5）

    （3）﹣4×（﹣3）2+5×（﹣2）﹣6

    （4）（1﹣+）×（﹣48）

    （5）﹣22+[（﹣4）2﹣（1﹣3）×3]

    （6）（﹣125）÷（﹣5）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四个全等的直角三角形纸片既可以拼成（内角不是直角）的菱形ABCD，也可以拼成正方形EFGH，则菱形ABCD面积和正方形EFGH面积之比为（ ）
    A.1
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案