


 ,∠CAC′=
,∠CAC′= ,试探索
,试探索 、
、 满足什么关系时,△ACE与△FBE是全等三角形,并说明理由。
满足什么关系时,△ACE与△FBE是全等三角形,并说明理由。 (2)可知△CAC′∽△BAB′,∴∠ACE=∠EBF,而∠AEC=∠BEF
(2)可知△CAC′∽△BAB′,∴∠ACE=∠EBF,而∠AEC=∠BEF
 =
= 时△ACE≌△FBE。
时△ACE≌△FBE。

 =2
=2 时,△ACE与△FBE全等
时,△ACE与△FBE全等

 =
= ,∠ABC=
,∠ABC= ,∴∠BCE=∠ABC
,∴∠BCE=∠ABC

科目:初中数学 来源:不详 题型:单选题
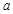 、b、c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③
、b、c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③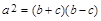 ;④
;④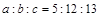 ,其中能判断△ABC是直角三角形的个数有( )
,其中能判断△ABC是直角三角形的个数有( )| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
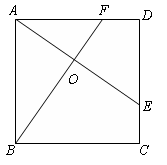
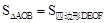 中正确的有
中正确的有查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.①正确,②错误 | B.①错误,②正确 | C.①,②都错误 | D.①,②都正确 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

A.8或 | B.10或 | C.10或 | D.8或 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
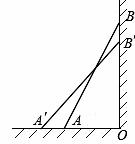
| A.等于1m | B.大于1m | C.小于1m | D.以上答案都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com