
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
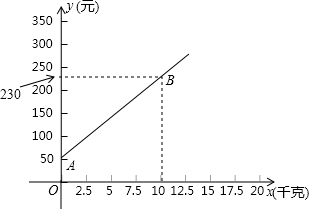 我县甲、乙两家甜橘柚基地生产的甜橘柚品质相同,销售价格也相同.“元旦”期间,两家均推出了优惠方案,甲基地的优惠方案是:每个游客进园需购买门票,采摘的甜橘柚打六折优惠;乙基地的优惠方案是:每个游客进园不需购买门票,采摘园的甜橘柚超过10千克后,超过部分打五折优惠.优惠期间,设某游客的甜橘柚采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中射线AB表示y1与x之间的函数关系.
我县甲、乙两家甜橘柚基地生产的甜橘柚品质相同,销售价格也相同.“元旦”期间,两家均推出了优惠方案,甲基地的优惠方案是:每个游客进园需购买门票,采摘的甜橘柚打六折优惠;乙基地的优惠方案是:每个游客进园不需购买门票,采摘园的甜橘柚超过10千克后,超过部分打五折优惠.优惠期间,设某游客的甜橘柚采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中射线AB表示y1与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD的顶点A的坐标为(0,3),顶点B在轴的正方向上,tan∠OBA=3,对角线AC,BD交于点P,射线OP交AB于点N,交DC于点M,点R从O出发沿OM方向以每秒$\sqrt{2}$个单位的速度运动,运动时间为t.
如图,正方形ABCD的顶点A的坐标为(0,3),顶点B在轴的正方向上,tan∠OBA=3,对角线AC,BD交于点P,射线OP交AB于点N,交DC于点M,点R从O出发沿OM方向以每秒$\sqrt{2}$个单位的速度运动,运动时间为t.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
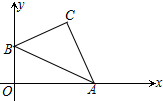 在平面直角坐标系中,已知点A、B的坐标分别为A(6,0)、B(0,2),以AB为斜边在右上方作Rt△ABC.设点C坐标为(x,y),则(x+y)的最大值=4+2$\sqrt{5}$.
在平面直角坐标系中,已知点A、B的坐标分别为A(6,0)、B(0,2),以AB为斜边在右上方作Rt△ABC.设点C坐标为(x,y),则(x+y)的最大值=4+2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,甲、乙两楼楼顶上的点A和点E与地面上的点C这三点在同一条直线上,点B、D分别在点E、A的正下方且D、B、C三点在同一条直线上,B、C相距50米,D、C相距80米,乙楼高BE为20米,求甲楼高AD.
如图,甲、乙两楼楼顶上的点A和点E与地面上的点C这三点在同一条直线上,点B、D分别在点E、A的正下方且D、B、C三点在同一条直线上,B、C相距50米,D、C相距80米,乙楼高BE为20米,求甲楼高AD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
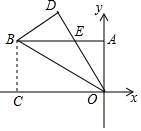 长方形OABC在平面直角坐标系内的位置如图所示,将长方形沿BO折叠,使点C落在点D处,DO与AB交于点E,BC=4cm,BA=8cm,则点E的坐标为( )
长方形OABC在平面直角坐标系内的位置如图所示,将长方形沿BO折叠,使点C落在点D处,DO与AB交于点E,BC=4cm,BA=8cm,则点E的坐标为( )| A. | (-3,4) | B. | (-3.5,4) | C. | (-3.7,4) | D. | (-4,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com