
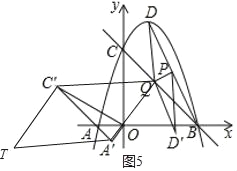
����Ŀ����ͼ1����֪������y����x2+2x+3��x�ύ��A��B���㣬��y�ύ�ڵ�C������ΪD������BC
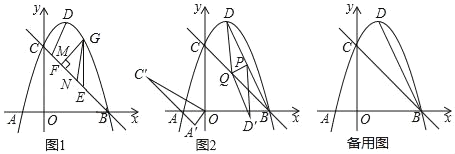
��1����G��ֱ��BC�Ϸ���������һ���㣨����B��C�غϣ�������G��y���ƽ���߽�ֱ��BC�ڵ�E����GF��BC�ڵ�F����M��N���߶�BC���������㣬��MN��EF������DM��GN������GEF���ܳ����ʱ����DM+MN+NG����Сֵ��
��2����ͼ2������BD����P���߶�BD���е㣬��Q���߶�BC��һ���㣬����DQ������DPQ��PQ���ۣ����߶�D��P���е�ǡ�������߶�BQ�ϣ�����AOC�Ƶ�O��ʱ����ת60��õ���A��OC�䣬��TΪ����ƽ����һ�㣬���Ե�Q��A�䡢C�䡢TΪ������ı�����ƽ���ı���ʱ�����T�����꣮
���𰸡���1��DM+MN+NG��СֵΪ![]() ����2����T������Ϊ��
����2����T��������![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��������
��1���������B��C��D�����꣬����ֱ��BC����ʽ�ҵõ���OCB��45������GE��y���GF��BC�ɵ���GEF�ǵ���ֱ�������Σ���GE���ʱ���ܳ�������G����Ϊ��a����a2+2a+3�������E��a����a+3�������е�GE��a�ĺ�����ϵʽ���䷽����������ֵ���õ���ʱ��G�����EF�ij������õ�MN������DM+MN+NG��Сֵת��Ϊ��DM+NG��Сֵ������D����ֱ��BC�ĶԳƵ�D1����ͨ��ƽ��MD1��D2�������������������Ļ���ͼ����⣮
��2���ɷ��۵�DD'��PQ��PD��PD'������PΪBD�е�֤����BD'D��90������PQ��BD'����D'P�е�H��BQ�ϣ���֤��PQH�ա�D'BH��������D'Q��BP���ı���DQD'PΪ���Σ���DQ��DP����Q������Ϊ��q����q+3�������з�����ã��ٸ�������ѵ�A'��C'������Ե�Q��A����C����TΪ������ı�����ƽ���ı��Σ�Ҫ���з������ۣ����ͼ�Σ�����ƽ���ı��ζԱ�ƽ�е����ʣ���ƽ������ķ���������õ�T��
��1��y����x2+2x+3������x��3����x+1��������x��1��2+4
����������x�ύ�ڵ�A����1��0������B��3��0������y�ύ�ڵ�C��0��3��������D��1��4����
��ֱ��CB����ʽ��y����x+3����BCO��45��
��GE��y�ᣬGF��BC
���GEF����BCO��45������GFE��90��
���GEF�ǵ���ֱ�������Σ�![]() ��
��
��C��GEF��EF+FG+GE����![]() +1��GE
+1��GE
���G��a����a2+2a+3�������E��a����a+3��������0��a��3
��GE����a2+2a+3������a+3������a2+3a![]()
��a![]() ʱ��GE�����ֵΪ
ʱ��GE�����ֵΪ![]() ��
��
���GEF���ܳ����ʱ�� ![]()
��![]() E��ɿ�����F����ƽ��
E��ɿ�����F����ƽ��![]() ����λ������ƽ��
����λ������ƽ��![]() ����λ
����λ
��ͼ1������D����ֱ��BC�ĶԳƵ�D1����1��2������N��ND2��D1M��ND2��D1M
��DM��D1M��ND2�� ![]() ,��
,��![]()
��DM+MN+NG��MN+ND2+NG
����D2��N��G��ͬһֱ����ʱ��ND2+NG��D2GΪ��Сֵ
��
��DM+MN+NG��СֵΪ![]()
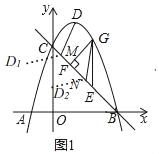
��2������DD'��D'B����D'P��BQ����ΪH����ͼ2��
�ߡ���DPQ��PQ���۵���D'PQ
��DD'��PQ��PD��PD'��DQ��D'Q����DQP����D'QP
��PΪBD�е�
��PB��PD��PD'��P��2��2��
���BDD'��ֱ�������Σ���BD'D��90��
��PQ��BD'
���PQH����D'BH
��HΪD'P�е�
��PH��D'H
����PQH����D'BH��
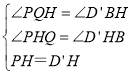
���PQH�ա�D'BH��AAS��
��PQ��BD'
���ı���BPQD'��ƽ���ı���
��D'Q��BP
���DPQ����D'QP
���DQP����DPQ
��DQ��DP
��DQ2��DP2����2��1��2+��2��4��2��5
��Q��q����q+3����0��q��3��
����q��1��2+����q+3��4��2��5
��ã�![]() ����ȥ��
����ȥ��
����Q����Ϊ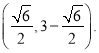
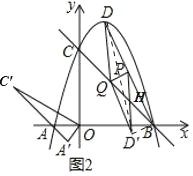
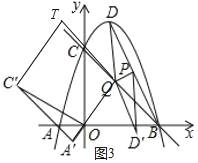
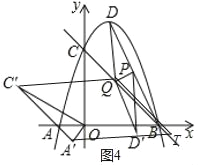
�ߡ�AOC�Ƶ�O��ʱ����ת60���õ���A��OC��
��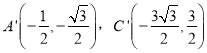
��A'��C'�������Ϊ![]() ���������Ϊ
���������Ϊ![]()
A'��Q�������Ϊ![]() ���������Ϊ
���������Ϊ![]()
����ƽ���ı���A'C'TQʱ����ͼ3������T������Ϊ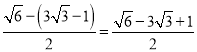 ��������Ϊ
��������Ϊ![]()
����ƽ���ı���A'C'QTʱ����ͼ4������T������Ϊ![]() ��������Ϊ
��������Ϊ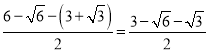
����ƽ���ı���A'TC'Qʱ����ͼ5������T������Ϊ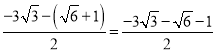 ��������Ϊ
��������Ϊ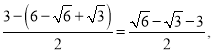
������������T��������![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ����һ����Ȼ���ĸ�λ���ֽ�ȥ���������µ�����ȥ��λ����2�����������7�ı�������ԭ���ܱ�7����.�����̫�������Ƿ�7�ı��������ظ���������β��������������Ĺ��̣�ֱ��������ж�Ϊֹ�����磬�ж�392�Ƿ�7�ı����Ĺ������£�![]() ��
��![]() �����ԣ�392��7�ı������������ж�8638�Ƿ�7�ı����Ĺ������£�
�����ԣ�392��7�ı������������ж�8638�Ƿ�7�ı����Ĺ������£�![]() ��
��![]() ��
��![]() �����ԣ�8638��7�ı�����
�����ԣ�8638��7�ı�����
���϶�����һ����λ��Ȼ��n����ǧλ���λ��ͬ����λ��ʮλ��ͬ�����dz������Ϊ���Գ������������Գ�����n��ǰ��λ�����λ����λ�õõ�һ���µ����Գ�����![]() ����
����![]() ������
������![]() ��
��
(1)���ò���һ�ķ����ж�6909��367�ܲ��ܱ�7������
(2)��m��p�����Գ�����������![]() ��
��![]() ��
��![]() ��
��![]() ��a��b��c��Ϊ����������m�ܱ�7��������
��a��b��c��Ϊ����������m�ܱ�7��������![]() ����p��
����p��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣�ͼ�����A����3��0�����Գ���Ϊֱ��x=��1���������½��ۣ���ab��0����b2��4ac��0����4b+c��0������B����![]() ��y1����C����
��y1����C����![]() ��y2��Ϊ����ͼ���ϵ����㣬��y1��y2��������3��x��1ʱ��y��0��������ȷ�Ľ����ǣ�������
��y2��Ϊ����ͼ���ϵ����㣬��y1��y2��������3��x��1ʱ��y��0��������ȷ�Ľ����ǣ�������

A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������ÿ̨���۷ֱ�Ϊ2000Ԫ��1700Ԫ��A��B�����ͺŵĿյ�������ǽ����ܵ����������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 5̨ | 18000Ԫ |
�ڶ��� | 4̨ | 10̨ | 31000Ԫ |
�����ۡ��ۼ۾����ֲ��䣬������������������ɱ���
��1����A��B�����ͺŵĿյ������۵��ۣ�
��2�����������ò�����54000Ԫ�Ľ���ٲɹ��������ͺŵĿյ���30̨����A���ͺŵĿյ�����ܲɹ�����̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��չ���������Ρ��ж���Ϊ����İ�ӻ�������������2������ѧ��ȤС�������5����Ҫ�۵㲢�ڱ���ѧ���н����˵��飨Ҫ��ÿλͬѧֻѡ�Լ����Ͽɵ�һ��۵㣩�����Ƴ�����������ͳ��ͼ��

��1���ð����� ���ˣ�ѧ��ѡ������г���۵������ ���ˣ�������ͳ��ͼ�У�����г���۵��������������Բ�Ľ����� ���ȣ�
��2�������У��360������ѧ����������������ѡ�����ж����۵�ij���ѧ��Լ���� ���ˣ�
��3�������ѧ��ȤС������5����Ҫ�۵�����ѡ����۵���ȫУѧ���н��е��飬��ǡ��ѡ������г�������ж����۵�ĸ��ʣ�����״ͼ���б���������𣩣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
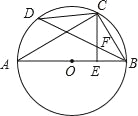
����Ŀ����ͼ��AB�ǡ�O��ֱ������C�ڡ�O�ϣ�CE��AB��E��BD��CE�ڵ�F��CF��BF��
��1����֤��C��![]() ���е㣻
���е㣻
��2����CD��4��AC��8�����O�İ뾶Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
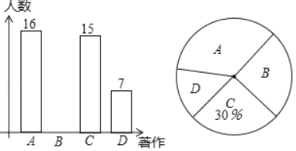
����Ŀ��ijУ��A����ʫ����B���δʡ���C����ɽͯ�ϡ���D������������������չ�����ܻ�ӭ�Ĵ�ͳ�Ļ����������飬���������������ѧ����ÿ��ѧ����ѡ��ֻ��ѡ�����������е�һ�֣������õ�����Ϣ����������������������ͳ��ͼ��
��1����һ�������˶�����ѧ����
��2���뽫����ͳ��ͼ����������
��3����У������ʦ������������������ѡȡ������Ϊѧ�����ٱض��鼮��������״ͼ���б��ķ�����ǡ��ѡ�С��δʡ��͡���ɽͯ�ϡ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬O��AB��һ�㣬��OAΪ�뾶�ġ�O��BC�����ڵ�D����AB���ڵ�E������ED���ӳ���AC���ӳ����ڵ�F��
��1����֤��AE=AF��
��2����DE=3��sin��BDE=![]() ����AC�ij���
����AC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
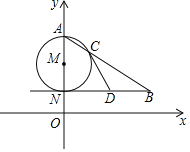
����Ŀ����ͼ��AN����M��ֱ����NB��x�ᣬAB����M�ڵ�C��
��1������A��0��6����N��0��2������ABN=30�㣬���B�����ꣻ
��2����DΪ�߶�NB���е㣬��֤��ֱ��CD����M�����ߣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com