
【题目】如图,在△ABC中,∠ACB=90°,O是AB上一点,以OA为半径的⊙O与BC相切于点D,与AB交于点E,连接ED并延长交AC的延长线于点F.
(1)求证:AE=AF;
(2)若DE=3,sin∠BDE=![]() ,求AC的长.
,求AC的长.

【答案】(1)证明见解析;(2)8.
【解析】
(1)根据切线的性质和平行线的性质解答即可;
(2)根据直角三角形的性质和三角函数解答即可.
(1)连接OD,
∵OD=OE,
∴∠ODE=∠OED.
∵直线BC为⊙O的切线,
∴OD⊥BC.
∴∠ODB=90°.
∵∠ACB=90°,
∴OD∥AC.
∴∠ODE=∠F.
∴∠OED=∠F.
∴AE=AF;
(2)连接AD,
∵AE是⊙O的直径,
∴∠ADE=90°,
∵AE=AF,
∴DF=DE=3,
∵∠ACB=90°,
∴∠DAF+∠F=90°,∠CDF+∠F=90°,
∴∠DAF=∠CDF=∠BDE,
在Rt△ADF中,![]() =sin∠DAF=sin∠BDE=
=sin∠DAF=sin∠BDE=![]() ,
,
∴AF=3DF=9,
在Rt△CDF中,![]() =sin∠CDF=sin∠BDE=
=sin∠CDF=sin∠BDE=![]() ,
,
∴CF=![]() DF=1,
DF=1,
∴AC=AF﹣CF=8.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】已知:如图16,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式.
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b与反比例函数y=![]() 的图象交于A(1,4),B(﹣2,n)两点.
的图象交于A(1,4),B(﹣2,n)两点.
(1)求m和n的值;
(2)求k和b的值;
(3)结合图象直接写出不等式![]() -kx﹣b>0的解集.
-kx﹣b>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
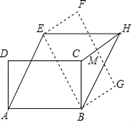
【题目】如图,矩形ABCD中,AB=3,AD=![]() ,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM=( )
,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM=( )
A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
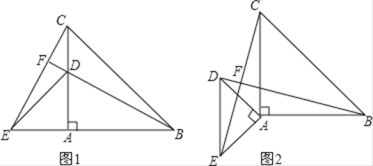
【题目】如图,在图1中,△ABC与△ADE,![]() ,AC=AB,AD=AE,点D在AC上,连接BD并延长BD交CE于点F.
,AC=AB,AD=AE,点D在AC上,连接BD并延长BD交CE于点F.
(1)请判断BD与CE是否相等;(直接写出结论,不需说明理由)
(2)求∠BFC的度数;(直接写出结论,不需说明理由)
(3)将△ADE按逆时针方向旋转一定角度,如图2,连接BD,CE交于点F.(1)、(2)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实视力保护工作,某校组织七年级学生开展了视力保健活动.活动前随机测查了30名学生的视力,活动后再次测查这部分学生的视力.两次相关数据记录如下:
活动前被测查学生视力数据:
4.0,4.1,4.1,4.2,4.2,4.3,4.3,4.4,4.4,4.4,4.5,4.5,4.6,4.6,4.6
4.7,4.7,4.7,4.7,4.8,4.8,4.8,4.8,4.8,4.9,4.9,4.9,5.0,5.0,5.1
活动后被测查学生视力数据:
4.0,4.2,4.3,4.4,4.4,4.5,4.5,4.6,4.6,4.6,4.7,4.7,4.7,4.7,4.8
4.8,4.8,4.8,4.8,4.8,4.8,4.9,4.9,4.9,4.9,4.9,5.0,5.0,5.1,5.1
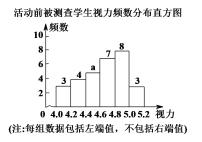

根据以上信息回答下列问题:
(1)填空:a= ,b= ,活动前被测查学生视力样本数据的中位数是 ,活动后被测查学生视力样本数据的众数是 ;
(2)若视力在4.8及以上为达标,估计七年级600名学生活动后视力达标的人数有多少?
(3)分析活动前后相关数据,从一个方面评价学校开展视力保健活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个相似三角形的面积比为![]() ,周长和是
,周长和是![]() ,则这两个三角形的周长分别是( )
,则这两个三角形的周长分别是( )
A. 8cm和12cm B. 7cm和13cm C. 9cm和11cm D. 6cm和14cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com