
【题目】某校开展了以“责任、感恩”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图,

(1)该班有 人,学生选择“和谐”观点的有 人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是 度;
(2)如果该校有360名初三学生,利用样本估计选择“感恩”观点的初三学生约有 人;
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答).
【答案】(1) 40,4,36;(2) 90(人)(3)![]() .
.
【解析】
(1)根据选择进取的人数是12,占总人数的30%,据此即可求得总人数;总人数乘以选择“和谐”观点的比例即可求得选择“和谐”观点的人数;选择“和谐”观点的百分比乘以360°,即可求得,“和谐”观点所在扇形区域的圆心角;
(2)总人数360乘以选择“感恩”观点比例,即可求得;
(3)设平等、进取、和谐、感恩、互助分别用ABCDE表示.利用树状图表示,即可利用概率公式求解.
(1)该班的总人数是:12÷30%=40(人);
选择“和谐”观点的有40×10%=4(人);
“和谐”观点所在扇形区域的圆心角是360°×10%=36°;
(2)该校有360名初三学生,利用样本估计选择“感恩”观点的初三学生约有:360×25%=90(人);
(3)设平等、进取、和谐、感恩、互助分别用ABCDE表示.利用树状图表示:

共有20种情况,选择和谐、感恩的有2种情况,因而恰好选到“和谐”和“感恩”观点的概率是:![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,一超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1∶2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为37°,则二楼的层高BC约为(精确到0.1米,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)( )

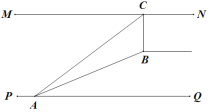
图1 图2
A. 4米 B. 3.6米 C. 2.2米 D. 4.6米
查看答案和解析>>
科目:初中数学 来源: 题型:
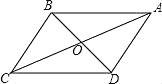
【题目】已知平行四边形ABCD中,如图,对角线AC和BD相交于点O,AC=10,BD=8.
(1)若AC⊥BD,试求四边形ABCD的面积;
(2)若AC与BD的夹角∠AOD=60°,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD在平面直角坐标系的第一象限内,BC与x轴平行,AB=1,点C的坐标为(6,2),E是AD的中点;反比例函数y1=![]() (x>0)图象经过点C和点E,过点B的直线y2=ax+b与反比例函数图象交于点F,点F的纵坐标为4.
(x>0)图象经过点C和点E,过点B的直线y2=ax+b与反比例函数图象交于点F,点F的纵坐标为4.
(1)求反比例函数的解析式和点E的坐标;
(2)求直线BF的解析式;
(3)直接写出y1>y2时,自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家生产一种新型电子产品,制造时每件的成本为40元,通过试销发现,销售量![]() 万件
万件![]() 与销售单价
与销售单价![]() 元
元![]() 之间符合一次函数关系,其图象如图所示.
之间符合一次函数关系,其图象如图所示.
![]() 求y与x的函数关系式;
求y与x的函数关系式;
![]() 物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润
物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润![]() 最大?最大利润是多少?
最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于点C,顶点为D,连接BC
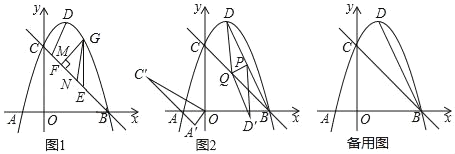
(1)点G是直线BC上方抛物线上一动点(不与B、C重合),过点G作y轴的平行线交直线BC于点E,作GF⊥BC于点F,点M、N是线段BC上两个动点,且MN=EF,连接DM、GN.当△GEF的周长最大时,求DM+MN+NG的最小值;
(2)如图2,连接BD,点P是线段BD的中点,点Q是线段BC上一动点,连接DQ,将△DPQ沿PQ翻折,且线段D′P的中点恰好落在线段BQ上,将△AOC绕点O逆时针旋转60°得到△A′OC′,点T为坐标平面内一点,当以点Q、A′、C′、T为顶点的四边形是平行四边形时,求点T的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山种植某产品种蜜柚![]() 已知该蜜柚的成本价为8元
已知该蜜柚的成本价为8元![]() 千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量
千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量![]() 千克
千克![]() 与销售单价
与销售单价![]() 元
元![]() 千克
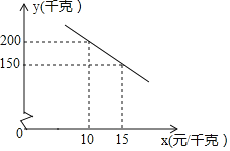
千克![]() 之间的函数关系如图所示.
之间的函数关系如图所示.
![]() 求y与x的函数关系式,并写出x的取值范围;
求y与x的函数关系式,并写出x的取值范围;
![]() 当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
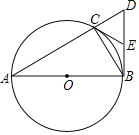
【题目】如图,已知△ABC内接于⊙O,AB为⊙O的直径,BD⊥AB,交AC的延长线于点D.
(1)E为BD的中点,连结CE,求证:CE是⊙O的切线;
(2)若AC=3CD,求∠A的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解全校400名学生参加课外锻炼的情况,随机对40名学生一周内平均每天参加课外锻炼的时间进行了调查,结果如下:(单位:分)
40 21 35 24 40 38 23 52 35 62 36 15 51 45 40 42 40 32 43 36
34 53 38 40 39 32 45 40 50 45 40 40 26 45 40 45 35 40 42 45
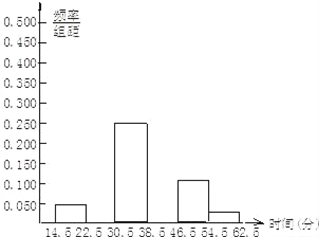
(1)补全频率分布表和频率分布直方图.
分组 | 频数 | 频率 |
4.5﹣22.5 | 2 | 0.050 |
22.5﹣30.5 | 3 | |
30.5﹣38.5 | 10 | 0.250 |
38.5﹣46.5 | 19 | |
46.5﹣54.5 | 5 | 0.125 |
54.5﹣62.5 | 1 | 0.025 |
合计 | 40 | 1.000 |
(2)填空:在这个问题中,总体是____,样本是____.由统计结果分析的,这组数据的平均数是38.35(分),众数是____,中位数是_____.
(3)如果描述该校400名学生一周内平均每天参加课外锻炼时间的总体情况,你认为用平均数、众数、中位数中的哪一个量比较合适?
(4)估计这所学校有多少名学生,平均每天参加课外锻炼的时间多于30分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com